
 =(2,sinθ),
=(2,sinθ),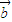 =(1,cosθ),θ为锐角.
=(1,cosθ),θ为锐角.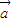 •
• =
=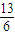 ,求sinθ+cosθ的值;
,求sinθ+cosθ的值;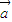 ∥
∥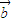 ,求sin(2θ+
,求sin(2θ+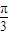 )的值.
)的值. .再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;
.再由同角三角函数的平方关系,可得(sinθ+cosθ)2的值,结合θ为锐角,开方即得sinθ+cosθ的值;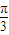 )的值.
)的值.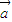 •
•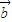 =2+sinθcosθ=
=2+sinθcosθ=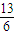 ,∴sinθcosθ=
,∴sinθcosθ= . …(2分)
. …(2分) .
.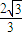 (舍负). …(5分)
(舍负). …(5分)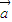 ∥
∥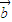 ,
,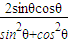 =
=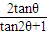 =
=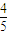 ,
,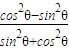 =
=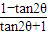 =-
=-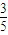 .…(11分)
.…(11分)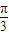 )=
)= sin2θ+
sin2θ+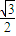 cos2θ=
cos2θ= ×
×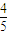 +
+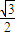 ×(-
×(-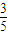 )=
)=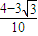 . …(14分)
. …(14分)

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 13 |
| 6 |
| a |
| b |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:南京二模 题型:解答题
| a |
| b |
| a |
| b |
| 13 |
| 6 |
| a |
| b |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| a |
| b |
| a |
| b |
| a |
| b |
| 13 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省泰安市高三(上)期末数学试卷(文科)(解析版) 题型:选择题
 ,
,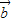 =(2,sinα),若
=(2,sinα),若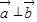 ,则tan(α-
,则tan(α-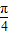 )等于( )
)等于( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com