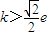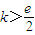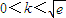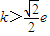分析:(1)对任意x1,x2∈[-1,1]都有f(x1)≥g(x2),等价于f(x)min≥g(x)max,进而转化为函数的最值问题;
(2)存在x1,x2∈[-1,1],使得f(x1)<g(x2),等价于f(x)min<g(x)max,进而转化为函数的最值问题.
解答:解:(1)f′(x)=3x
2-3=3(x+1)(x-1),
当x∈[-1,1]时,f′(x)≤0,所以f(x)在[-1,1]上单调递减,f(x)
min=f(1)=k-2;
g′(x)=
=
,
当x∈[-1,1]时,g′(x)≥0,所以g(x)在[-1,1]上单调递增,g(x)
max=g(1)=
.
对任意x
1,x
2∈[-1,1]都有f(x
1)≥g(x
2),等价于f(x)
min≥g(x)
max,
即k-2≥
,解得k≥3.
所以k的取值范围是[3,+∞).
(2)由(1)知:f(x)在[-1,1]上单调递减,f(x)
min=f(1)=k-2;
g(x)在[-1,1]上单调递增,g(x)
max=g(1)=
.
存在x
1,x
2∈[-1,1],使得f(x
1)<g(x
2),等价于f(x)
min<g(x)
max,
即k-2<
,解得0<k<3.
所以k的取值范围是(0,3).
点评:本题为不等式恒成立问题,解决的基本思路是转化为函数最值问题处理,从而可用导数解决.本题注意分析两问间的“否定”关系.