
(本小题共12分)如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,
F为CE上的点,且BF⊥平面ACE
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年黑龙江哈尔滨市高三第五次月考理科数学试卷(解析版) 题型:解答题
(本小题共12分)
如图,已知直线l与抛物线 相切于点P(2,1),且与x轴交于点A,O为坐标原点,
相切于点P(2,1),且与x轴交于点A,O为坐标原点,
定点B的坐标为(2,0).

(1)若动点M满足 ,求点M的轨迹C;
,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年黑龙江哈尔滨市高三第五次月考理科数学试卷(解析版) 题型:解答题
(本小题共12分)
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=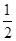 AD=1,CD=
AD=1,CD=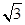 .
.
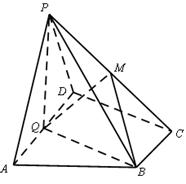
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市高三阶段考试(二)文科数学试卷(解析版) 题型:解答题
(本小题共12分)如图,四边形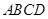 是矩形,
是矩形,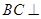 平面
平面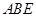 ,
,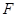 是
是 上一点,
上一点,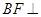 平面
平面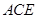 ,点
,点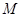 ,
,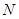 分别是
分别是 ,
,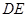 的中点.
的中点.
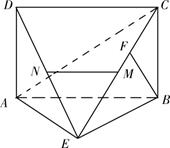
(Ⅰ)求证: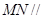 平面
平面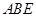 ;
;
(Ⅱ)求证: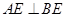 .
.
查看答案和解析>>
科目:高中数学 来源:2010年陕西省汉中市汉台区高二上学期期末数学文卷 题型:解答题
(本小题共12分)如图,△ACD是等边三角形,△ABC是等腰直角
三角形,∠ACB=90°,BD交AC于E,AB=2.
(1)求cos∠CBE的值;
(2)求AE。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com