定义一种运算△:n△m=n•am(m,n∈N,a≠0)
(1)若数列{an}(n∈N*)满足an=n△m,当m=2时,求证:数列{an}为等差数列;
(2)设数列{cn}(n∈N*)的通项满足cn=n△(n-1),试求数列{cn}的前n项和Sn.
【答案】
分析:(1)先求出通项公式,再写出第n+1项,证明第n+1项与第n项的差是个常数.
(2)写出c
n的表达式,当a=1时,数列{c
n}是个等差数列易求出它的前n项和,
当a≠1时,用错位相减法求出它的前n项和.
解答:(1)证明:由题意知当m=2时,a
n=n△m=a
2•n,
则有a
n+1=a
2•(n+1) (2分)
故有a
n+1-a
n=a
2,(n∈N
*),其中a
1=1△2=a
2,(3分)
所以数列{a
n}是以a
1=a
2为首项,公差d=a
2的等差数列.(4分)
(2)依题意有,c
n=n△(n-1)=n•a
n-1,(n∈N
*),(5分)
所以,当a=1时,
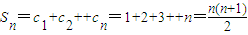
;(7分)
当a≠1时,S
n=1•a
+2•a
1++(n-1)•a
n-2+n•a
n-1,(1)
所以aS
n=1•a
1+2•a
2++(n-1)•a
n-1+n•a
n(2)(8分)
由(2)-(1)得:(1-a)S
n=1•a
+1•a
1++1•a
n-2+1•a
n-1-na
n(9分)
得:
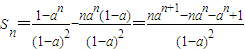
,(n∈N
*)(11分)
综上所述,
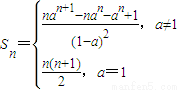
(14分)
点评:本题考查等差数列的通项公式及求和公式,以及用错位相减法对数列进行求和,体现分类讨论的数学思想.

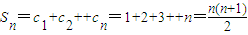 ;(7分)
;(7分)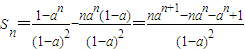 ,(n∈N*)(11分)
,(n∈N*)(11分)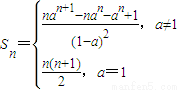 (14分)
(14分)
