
如图所示,平面![]() ∥平面
∥平面![]() ,点A∈
,点A∈![]() ,C∈
,C∈![]() ,点B∈
,点B∈![]() ,D∈
,D∈![]() ,点E,F分别在
,点E,F分别在 线段AB,CD上,且AE∶EB=CF∶FD.
线段AB,CD上,且AE∶EB=CF∶FD.
(1)求证:EF∥![]() ;
;
(2)若E,F分别是AB,CD的中点,AC=4,BD=6,且AC,BD所成的角为60°,
求EF的长.
(1)证明略(2)EF=![]() 或EF=
或EF=![]()
(1) ①当AB,CD在同一平面内时,
由![]() ∥
∥![]() ,平面
,平面![]() ∩平面ABDC=AC,
∩平面ABDC=AC,
平面![]() ∩平面ABDC=BD,∴AC∥BD, 2分
∩平面ABDC=BD,∴AC∥BD, 2分
∵AE∶EB=CF∶FD,∴EF∥BD,
又EF![]()
![]() ,BD
,BD![]()
![]() ,∴EF∥
,∴EF∥![]() . 4分
. 4分
②当AB与CD异面时,
设平面ACD∩![]() =DH,且DH=AC.
=DH,且DH=AC.
 ∵
∵![]() ∥
∥![]() ,
,![]() ∩平面ACDH=AC,
∩平面ACDH=AC,
∴AC∥DH,∴四边形ACDH是平行四边形, 6分
在AH上取一点G,使AG∶GH=CF∶FD,
又∵AE∶EB=CF∶FD,∴GF∥HD,EG∥BH,
又EG∩GF=G,∴平面EFG∥平面![]() .
.
∵EF![]() 平面EFG,∴EF∥
平面EFG,∴EF∥![]() .综上,EF∥
.综上,EF∥![]() . 8分
. 8分
(2)解 如图所示,连接AD,取AD的中点M,连接ME,MF.
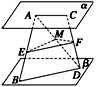 ∵E,F分别为AB,CD的中点,
∵E,F分别为AB,CD的中点,
∴ME∥BD,MF∥AC,
且ME=![]() BD=3,MF=
BD=3,MF=![]() AC=2,
AC=2,
∴∠EMF为AC与BD所成的角(或其补角),
∴∠EMF=60°或120°, 12分
∴在△EFM中由余弦定理得,
EF=![]()
=![]() =
=![]() ,
,
即EF=![]() 或EF=
或EF=![]() . 16分
. 16分


科目:高中数学 来源: 题型:
 如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E,F分别在线段AB,CD上,AB,CD所在直线异面,且AE:EB=CF:FD
如图所示,平面α∥平面β,点A∈α,C∈α,点B∈β,D∈β,点E,F分别在线段AB,CD上,AB,CD所在直线异面,且AE:EB=CF:FD查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期末考练习三理科数学试卷(解析版) 题型:解答题
如图所示,平面 ⊥平面
⊥平面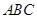 ,
, ,
,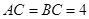 ,四边形
,四边形 是直角梯形,
是直角梯形, ,
, ,
,  ,
, 分别为
分别为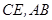 的中点.
的中点.
(Ⅰ) 用几何法证明: 平面
平面 ;
;
(Ⅱ)用几何法证明: 平面
平面 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com