解:(1)设-1≤x
1<x
2≤1,由奇函数的定义和题设条件,得
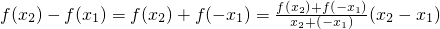
>0,
∴f(x)在[-1,1]上是增函数.
∵a,b∈[-1,1],且a>b,
∴f(a)>f(b).
(2)∵f(x)是[-1,1]上的增函数,
∴不等式
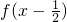
<
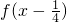
等价于
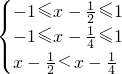
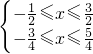
解得
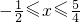
∴原不等式的解集是
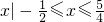
.
(3)设函数g(x),h(x)的定义域分别是P和Q,
则P={x|-1≤x-c≤1}=x|c-1≤x≤c+1},
Q={x|-1≤x-c
2≤1}={x|c
2-1≤x≤c
2+1}.
由P∩Q=∅可得c+1<c
2-1或c
2+1<c-1.
解得c的取值范围是(-∞,-1)∪(2,+∞).
分析:(1)由题意,可先证明函数的单调性,由奇定义和题设条件易得函数是增函数,由单调性比较两个函数值的大小即可;
(2)(1)由(1)函数f(x)是[-1,1]上的增函数上的增函数,可将不等式
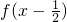
<
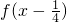
转化为
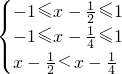
,解出它的解集即可得到不等式的解集;
(3)由题意,要先解出两个函数的定义域,得P={x|-1≤x-c≤1}=x|c-1≤x≤c+1},Q={x|-1≤x-c
2≤1}={x|c
2-1≤x≤c
2+1}. 由于此两个集合的解集是空集,比较两个集合的端点,得到关于参数c的不等式,解出c的取值范围.
点评:本题考查了单调性的判断,利用单调性比较大小,解不等式,求函数定义域及根据两集合间的包含关系确定参数的取值范围,本题是单调性运用综合题,解题的关键是判断出函数的单调性,熟练掌握单调性在比较大小与解不等式中的运用,本题中有一易错点,在第二小题中,易忘记定义域的限制条件,只由单调性转化出一个不等式,从而解出
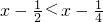
得到解集是R,转化时一定要注意等价.本题考查了转化的思想,判断推理的能力及计算能力

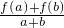 >0.
>0.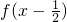 <
<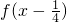 ;
;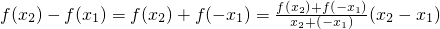 >0,
>0,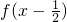 <
<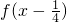 等价于
等价于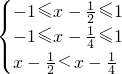
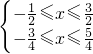 解得
解得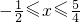
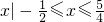 .
.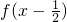 <
<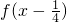 转化为
转化为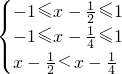 ,解出它的解集即可得到不等式的解集;
,解出它的解集即可得到不等式的解集;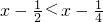 得到解集是R,转化时一定要注意等价.本题考查了转化的思想,判断推理的能力及计算能力
得到解集是R,转化时一定要注意等价.本题考查了转化的思想,判断推理的能力及计算能力 
