
 港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问检查站C离港口A有多远?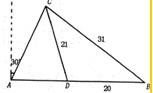 解:在△BDC中,CD=21海里,DB=20海里,BC=31海里,
解:在△BDC中,CD=21海里,DB=20海里,BC=31海里,| CD2+DB2-CB2 |
| 2CD•DB |
| 1 |
| 7 |
4
| ||
| 7 |
4
| ||
| 7 |
| CD |
| sin60° |
| AC |
| sin∠CDB |
| 21 | ||||
|
| AC | ||||
|


科目:高中数学 来源: 题型:
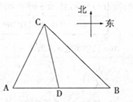 港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?查看答案和解析>>
科目:高中数学 来源: 题型:
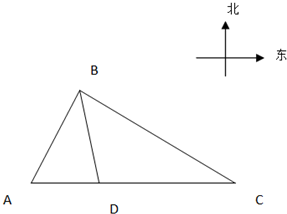 港口A北偏东30°方向的B处有一小岛,A正东方向的C处有一渔船,该渔船距岛B为31海里,现该渔船从C处沿着正西方向航行20海里到D处后出现机械故障最多只能航行12海里,此时测得渔船距离小岛B还有21海里,故只能继续向港口航去,问该渔船最终是否需要港口派船在海上救援?
港口A北偏东30°方向的B处有一小岛,A正东方向的C处有一渔船,该渔船距岛B为31海里,现该渔船从C处沿着正西方向航行20海里到D处后出现机械故障最多只能航行12海里,此时测得渔船距离小岛B还有21海里,故只能继续向港口航去,问该渔船最终是否需要港口派船在海上救援?查看答案和解析>>
科目:高中数学 来源: 题型:
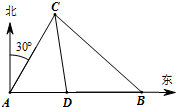 如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?
如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?查看答案和解析>>
科目:高中数学 来源:2010-2011年东北师大附中、哈师大附中、辽宁实验中学高二第二次考试数学理卷 题型:解答题
本小题满分12分)
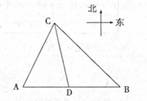
港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站为31海里,该轮船从B处沿正西方向航行20海里后到达D处观测站,已知观测站与检查站距离21海里,问此时轮船离港口A还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com