
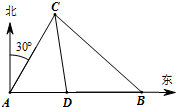
 如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?
如图所示,港口A北偏东30°方向的点C处有一观测站,港口正东方向的B处有一轮船,测得BC为31海里.该轮船从B处沿正西方向航行20海里后到达D处,测得CD为21海里.问此时轮船离港口A还有多少海里?| π |
| 3 |
| AD |
| sin∠ACD |
| CD |
| sin∠A |
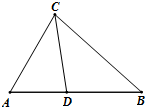 解:由题意可得,BC=31,BD=20,CD=21,A=60°
解:由题意可得,BC=31,BD=20,CD=21,A=60°| BD2+CD2-BC2 |
| 2×BD×CD |
| 202+212-312 |
| 2×21×20 |
| 1 |
| 7 |
| 1-cos2∠BDC |
4
| ||
| 7 |
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
5
| ||
| 14 |
| AD |
| sin∠ACD |
| CD |
| sin60° |
| CD×sin∠ACD |
| sin60° |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
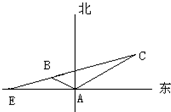 如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?查看答案和解析>>
科目:高中数学 来源: 题型:
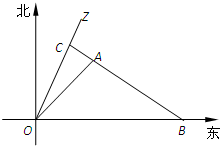 如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口
如图所示,一科学考察船从港口O出发,沿北偏东α角的射线OZ方向航行,而在离港口| 13 |
| 1 |
| 3 |
| 2 | ||
|
| 7 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.
如图所示,上午11时在某海岛上一观察点A测得一轮船在海岛北偏东60°的C处,12时20分测得船在海岛北偏西60°的B处,12时40分轮船到达了位于海岛正西方且距海岛5km的E港口,轮船始终以匀速直线前进.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第一学期第二次阶段考试数学 题型:解答题
(本小题满分15分)
如图所示,一科学考察船从港口 出发,沿北偏东
出发,沿北偏东 角的射线
角的射线 方向航行,而在离港口
方向航行,而在离港口 (
( 为正常数)海里的北偏东
为正常数)海里的北偏东 角的A处有一个供给科考船物资的小岛,其中
角的A处有一个供给科考船物资的小岛,其中 ,
, .现指挥部需要紧急征调沿海岸线港口
.现指挥部需要紧急征调沿海岸线港口 正东m(
正东m( )海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
)海里的B处的补给船,速往小岛A装运物资供给科考船,该船沿BA方向全速追赶科考船,并在C处相遇.经测算当两船运行的航向与海岸线OB围成的三角形OBC的面积最小时,这种补给最适宜.
⑴ 求S关于m的函数关系式 ;
;
⑵ 应征调m为何值处的船只,补给最适宜.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com