
已知点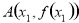 ,
,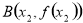 是函数
是函数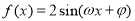
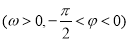 图象上的任意两点,且角
图象上的任意两点,且角 的终边经过点
的终边经过点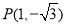 ,若
,若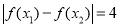 时,
时,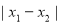 的最小值为
的最小值为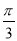 .
.
(1)求函数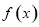 的解析式;
的解析式;
(2)求函数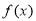 的单调递增区间;
的单调递增区间;
(3)求当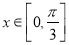 时,
时,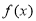 的值域.
的值域.
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源:2016届广西河池高中高三上第五次月考文科数学试卷(解析版) 题型:解答题
在直角坐标系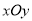 中,以
中,以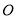 为极点,
为极点,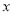 轴正半轴为极轴建立极坐标系.圆
轴正半轴为极轴建立极坐标系.圆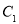 ,直线
,直线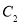 的极坐标方程分别为
的极坐标方程分别为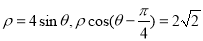 .
.
(Ⅰ)求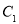 与
与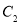 交点的极坐标;
交点的极坐标;
(Ⅱ)设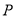 为
为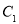 的圆心,
的圆心,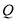 为
为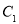 与
与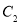 交点连线的中点.已知直线
交点连线的中点.已知直线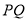 的参数方程为
的参数方程为 (
(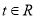 为参数),求
为参数),求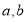 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高二上期中文科数学试卷(解析版) 题型:选择题
设双曲线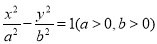 的一条渐近线与抛物线
的一条渐近线与抛物线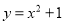 只有一个公共点,则双曲线的离心率为( )
只有一个公共点,则双曲线的离心率为( )
A.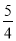 B.5 C.
B.5 C.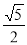 D.
D.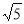
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省高二上第一次段考文数学卷(解析版) 题型:解答题
某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)在给出的坐标系中,画出关于x、y两个相关变量的散点图.

(2)请根据上表提供的数据,用最小二乘法求出变量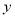 关于变量
关于变量 的线性回归直线方程
的线性回归直线方程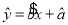 .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克).
(参考公式: ,
,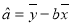 ,
, ,
, ,
, ,
,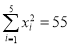
查看答案和解析>>
科目:高中数学 来源:2016届浙江省高三上学期期中文科数学试卷(解析版) 题型:解答题
已知向量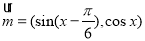 ,
, ,若函数
,若函数 .
.
(1)求 时,函数
时,函数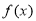 的值域;
的值域;
(2)在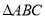 中,
中,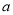 ,
,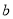 ,
,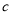 分别是角
分别是角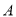 ,
, ,
,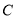 的对边,若
的对边,若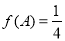 且
且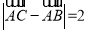 ,求
,求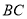 边上中线长的最大值.
边上中线长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com