
 +
+ =1上一动点,点H是点M在x轴上的射影,坐标平面xOy内动点M满足:
=1上一动点,点H是点M在x轴上的射影,坐标平面xOy内动点M满足: (O为坐标原点),设动点M的轨迹为曲线C.
(O为坐标原点),设动点M的轨迹为曲线C. =
= ,点E关于x轴的对称点为G,求直线GD的方程.
,点E关于x轴的对称点为G,求直线GD的方程.
 (O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆
(O为坐标原点),得出坐标之间的关系,利用P(x,y)是椭圆 +
+ =1上一动点,即可求出曲线C的方程;
=1上一动点,即可求出曲线C的方程; =
= ,得坐标之间的关系,联立
,得坐标之间的关系,联立 ,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k=
,得(1+k2)x2-2k2x+k2-4=0,利用韦达定理,即可求得k= ,
, ,
, ,再分
,再分 ,
, 分别求得求直线GD的方程.
分别求得求直线GD的方程. 解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0),
解:(Ⅰ)设动点M(x,y),P(x,y),则H(x,0), (O为坐标原点),即
(O为坐标原点),即

 +
+ =1上一动点
=1上一动点

 =
= ,
,
 ,得(1+k2)x2-2k2x+k2-4=0,
,得(1+k2)x2-2k2x+k2-4=0, ,…①x1x2=
,…①x1x2= ,…②,
,…②, ,…③
,…③ ,…④
,…④ ,
, …(9分)
…(9分) ,
, 时,
时, ,
, ,
, ,
,
 ,
, ,即
,即 ;
; 时,同理可求直线GD的方程是
时,同理可求直线GD的方程是 …(12分)
…(12分)

科目:高中数学 来源: 题型:
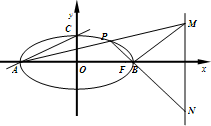 如图,设点P是椭圆E:
如图,设点P是椭圆E:| x2 |
| 4 |
| 10 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
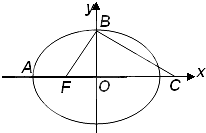 (2009•泰安一模)如图,点F是椭圆
(2009•泰安一模)如图,点F是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
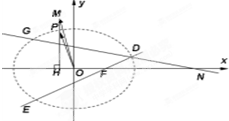 (2011•西山区模拟)如图,点P是椭圆
(2011•西山区模拟)如图,点P是椭圆| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| HM |
| HP |
| DF |
| FE |
查看答案和解析>>
科目:高中数学 来源: 题型:
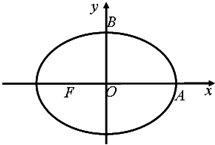 如图,点F是椭圆W:
如图,点F是椭圆W:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
3
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com