
如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P
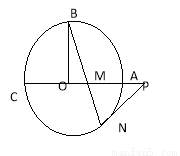
(1)求证: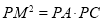
(2)若⊙O的半径为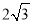 ,OA=
,OA=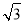 OM,求MN的长
OM,求MN的长
(1)证明见解析;(2)2.
【解析】
试题分析:
解题思路:(1)利用等腰三角形与切割线定理进行证明;(2)利用三角形的相似性进行求解.
规律总结:直线与圆的位置关系,是平面几何问题的常见题型,常考知识由:圆内接四边形、切割线定理、相似三角形、全等三角形等.
试题解析:(1)连结ON,则ON⊥PN,且△OBN为等腰三角形,
则∠OBN=∠ONB,∵∠PMN=∠OMB=900-∠OBN,∠PNM=900-∠ONB
∴∠PMN=∠PNM, ∴PM=PN
由条件,根据切割线定理,有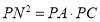
所以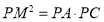
(2)OM=2,在Rt△BOM中,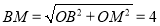
延长BO交⊙O于点D,连接DN
由条件易知△BOM∽△BND,于是
即 ,得BN=6
,得BN=6
所以MN=BN-BM=6-4=2.
考点:1.切割线定理;2.相似三角形.


科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试理科数学试卷(解析版) 题型:解答题
已知圆的极坐标方程为ρ2-4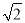 ρ·cos
ρ·cos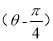 +6=0.
+6=0.
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点P(x,y)在该圆上,求x+y的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
设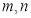 是不同的直线,
是不同的直线,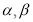 是不同的平面,下列命题中正确的是 ( )
是不同的平面,下列命题中正确的是 ( )
A.若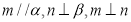 ,则
,则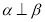
B.若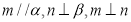 ,则
,则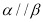
C.若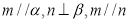 ,则
,则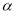 ⊥
⊥
D.若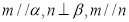 ,则
,则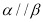
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
定义在R上的偶函数f(x)满足:对任意的 ,
,
有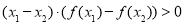 ,则当n∈N﹡时,有( ).
,则当n∈N﹡时,有( ).
A.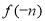 <
<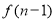 <
<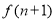 B.
B. <
<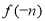 <
<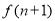
C. <
< <
<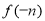 D.
D. <
< <
<
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某一批花生种子,若每1粒发芽的概率为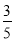 ,则播下3粒种子恰有2粒发芽的概率为( ).
,则播下3粒种子恰有2粒发芽的概率为( ).
A. 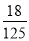 B.
B. 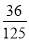 C.
C.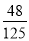 D.
D.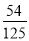
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:解答题
设△ABC的内角A、B、C所对的边分别为a、b、c,且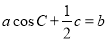 .
.
(1)求角A的大小; (2)若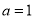 ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知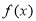 是定义在R上的奇函数,当
是定义在R上的奇函数,当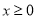 时
时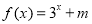 (m为常数),则
(m为常数),则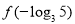 的值为( ).
的值为( ).
A.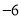 B.6 C.4 D.
B.6 C.4 D.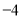
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标模块练习卷(解析版) 题型:解答题
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
附:
P(K2≥x0) | 0.050 | 0.010 | 0.001 |
x0 | 3.841 | 6.635 | 10.828 |
χ2=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com