
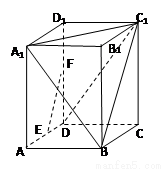
(本题满分10分) 在长方体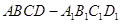 中,
中,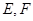 分别是
分别是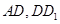 的中点,
的中点,
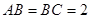 ,
,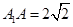 .
.
(Ⅰ)求证: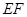 //平面
//平面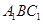 ;
;
(Ⅱ)在线段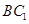 上是否存在点
上是否存在点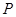 ,使直线
,使直线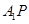 与
与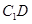 垂直,
垂直,
如果存在,求线段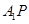 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
(Ⅰ)见解析;(Ⅱ)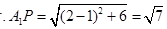 .
.
【解析】
试题分析:(1)根据已知中的长方体的性质,结合线线平行,得到线面平行的证明。
(2)由于根据已知条件可知线A1D1垂直于平面CD1,进而利用性质定理得到线线垂直,相似来求解长度。
解:(Ⅰ)连接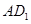 ,在长方体
,在长方体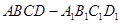 中,
中,
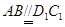 ,则四边形
,则四边形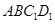 是平行四边形,∴
是平行四边形,∴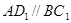 ,又∵
,又∵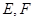 分别是
分别是 的中点∴
的中点∴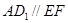 ,∴
,∴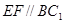 ,又
,又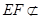 面
面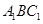 ,
,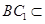 面
面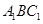 ,
,
∴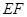 //平面
//平面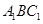 (3分)
(3分)
(Ⅱ)在平面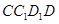 中作
中作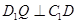 交
交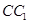 于
于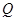 ,过
,过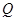 作
作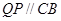 交
交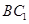 于点
于点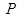 ,连
,连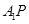 ∵
∵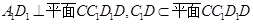
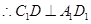
而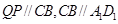
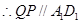 又
又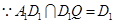
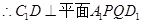 ∵
∵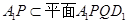
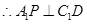
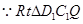 ∽
∽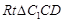
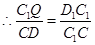
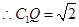
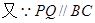
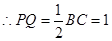
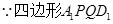 为直角梯形,且高
为直角梯形,且高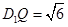
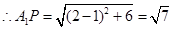 .(10分)
.(10分)
考点:本题主要是考查线面平行的判定以及线线垂直的证明运用。
点评:解决该试题的关键是熟练的利用线面平行的判定定理,得到线线平行进而得到证明,同时线面的垂直,结合相似得到求解。


科目:高中数学 来源:2011-2012学年上海市黄浦区高三上学期期终基础学业测评理科数学试卷 题型:解答题
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
选修4—4 参数方程与极坐标(本题满分10分)
已知圆![]() 和圆
和圆![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() .
.
(1)把圆![]() 和圆
和圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com