
已知中心在原点,对称轴为坐标轴的椭圆C的一个焦点在抛物线 的准线上,且椭圆C过点
的准线上,且椭圆C过点 .
.
(1)求椭圆C的方程;
(2)点A为椭圆C的右顶点,过点 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求 的取值范围.
的取值范围.
(1)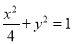 ;(2)
;(2)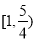 .
.
【解析】
试题分析:(1)由题设知椭圆中心在原点,一个焦点坐标为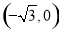 ,且过点
,且过点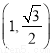 ,于是可设出其标准方程
,于是可设出其标准方程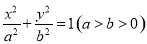 ,并用待定系数法求出
,并用待定系数法求出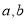 的值进而确定椭圆的方程.
的值进而确定椭圆的方程.
(2)当直线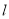 的斜率存在且不为零时,由题意可设直线
的斜率存在且不为零时,由题意可设直线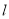 的方程为
的方程为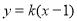 ,
,
与椭圆方程联立组成方程组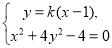 消去
消去 并结合韦达定理得到
并结合韦达定理得到 ,据此可将
,据此可将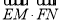 化成关于
化成关于 的函数而求解.
的函数而求解.
注意对直线 的斜率不存在及斜率为零的情况,要单独说明.
的斜率不存在及斜率为零的情况,要单独说明.
【解析】
(1)抛物线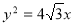 的准线方程为:
的准线方程为: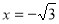 1分
1分
设椭圆的方程为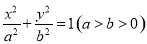 ,则
,则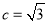
依题意得 ,解得
,解得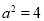 ,
,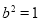 .
.
所以椭圆 的方程为
的方程为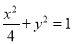 . 3分
. 3分
(2)显然点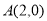 .
.
(1)当直线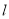 的斜率不存在时,不妨设点
的斜率不存在时,不妨设点 在
在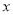 轴上方,
轴上方,
易得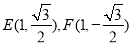 ,
,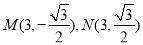 ,
,
所以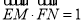 . 5分
. 5分
(2)当直线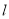 的斜率存在时,由题意可设直线
的斜率存在时,由题意可设直线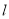 的方程为
的方程为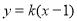 ,
,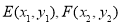 ,显然
,显然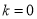 时,不符合题意.
时,不符合题意.
由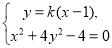 得
得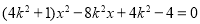 . 6分
. 6分
则 . 7分
. 7分
直线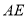 ,
,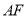 的方程分别为:
的方程分别为: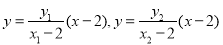 ,
,
令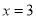 ,则
,则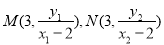 .
.
所以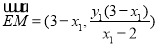 ,
,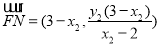 . 9分
. 9分
所以
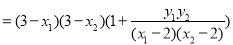
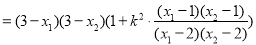
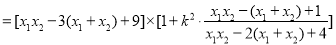
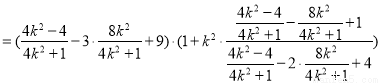
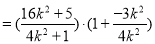
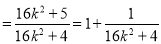 . 11分
. 11分
因为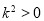 ,所以
,所以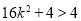 ,所以
,所以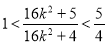 ,即
,即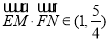 .
.
综上所述,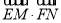 的取值范围是
的取值范围是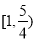 . 13分
. 13分
考点:1、椭圆的标准方程;2、抛物线的标准方程;3、直线与椭圆位置关系综合问题.


科目:高中数学 来源:2013-2014学年山东省烟台市高三5月适应性训练一理科数学试卷(解析版) 题型:解答题
已知等比数列{an}的前n项和Sn满足:S4-S1=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{an}为递增数列, ,
, ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三第二次模拟考试理科数学试卷(解析版) 题型:填空题
已知抛物线 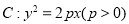 上一点
上一点 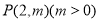 ,若P到焦点F的距离为4,则以P为圆心且与抛物线C的准线相切的圆的标准方程为_________.
,若P到焦点F的距离为4,则以P为圆心且与抛物线C的准线相切的圆的标准方程为_________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省潍坊市高三4月模拟考试文科数学试卷(解析版) 题型:选择题
为了调查学生携带手机的情况,学校对高一、高二、高三三个年级的学生进行分层抽样调查,已知高一有学生l000人、高二有1200人;三个年级总共抽取了66人,其中高一抽取了20人,则高三年级的全部学生数为( )
A.1000 B.1100 C.1200 D.1300
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:填空题
在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似的,我们在平面向量集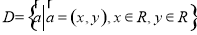 上也可以定义一个称“序”的关系,记为“
上也可以定义一个称“序”的关系,记为“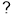 ”.定义如下:对于任意两个向量
”.定义如下:对于任意两个向量 当且仅当“
当且仅当“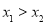 ”或“
”或“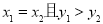 ”.按上述定义的关系“
”.按上述定义的关系“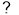 ”,给出如下四个命题:
”,给出如下四个命题:
①若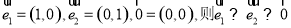 ;
;
②若 ,则
,则 ;
;
③若 ,则对于任意
,则对于任意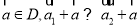 ;
;
④对于任意向量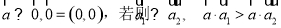 .
.
其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省淄博市高三复习阶段性诊断考试理科数学试卷(解析版) 题型:选择题
二项式 展开式中,x的幂指数是整数的项共有
展开式中,x的幂指数是整数的项共有
A.3项 B.4项 C.5项 D.6项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com