已知关于x的不等式x2-4x-m<0的非空解集为{x|n<x<5}
(1)求实数m和n的值
(2)求不等式loga(-nx2+3x+2-m)>0的解集.
【答案】
分析:(1)由题意得:n和5是方程x
2-4x-m=0的两个根结合根与系数的关系即可求得实数m和n的值;
(2)首先对a进行分类讨论:1°当a>1时,函数y=log
ax在定义域内单调递增;2°当0<a<1时,函数 y=log
ax在定义域内单调递减,分别求得它们的解集,最后综合得出:当a>1时原不等式的解集为:(-∞,-4)∪(1,+∞),当0<a<1时原不等式的解集为:(-4
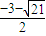
)∪
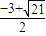
,1).
解答:解:(1)由题意得:n和5是方程x
2-4x-m=0的两个根(2分)
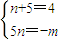
(3分)
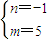
(1分)
(2)1°当a>1时,函数y=log
ax在定义域内单调递增
由log
a(-nx
2+3x+2-m)>0
得x
2+3x-3>1(2分)
即 x
2+3x-4>0
x>1 或 x<-4(1分)
2°当0<a<1时,函数 y=log
ax在定义域内单调递减
由:log
a(-nx
2+3x+2-m)>0
得:
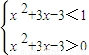
(2分)
即
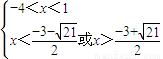
(1分)
-4<
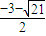
或
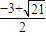
<x<1(1分)
∴当a>1时原不等式的解集为:(-∞,-4)∪(1,+∞),
当0<a<1时原不等式的解集为:(-4
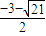
)∪
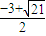
,1)(1分)
点评:本小题主要考查对数函数的单调性与特殊点、一元二次不等式的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

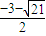 )∪
)∪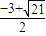 ,1).
,1).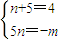 (3分)
(3分)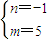 (1分)
(1分)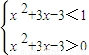 (2分)
(2分)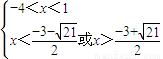 (1分)
(1分)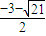 或
或 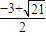 <x<1(1分)
<x<1(1分)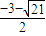 )∪
)∪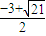 ,1)(1分)
,1)(1分)

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案 (1)几何证明选讲:如图,CB是⊙O的直径,AP是⊙O的切线,A为切点,AP与CB的延长线交于点P,若PA=8,PB=4,求AC的长度.
(1)几何证明选讲:如图,CB是⊙O的直径,AP是⊙O的切线,A为切点,AP与CB的延长线交于点P,若PA=8,PB=4,求AC的长度.