
[番茄花园1] 如图, 在矩形 中,点
中,点 分别
分别
在线段 上,
上,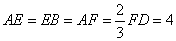 .沿直线
.沿直线
将  翻折成
翻折成 ,使平面
,使平面 .
.
(Ⅰ)求二面角 的余弦值;
的余弦值;
(Ⅱ)点 分别在线段
分别在线段 上,若沿直线
上,若沿直线 将四
将四
边形 向上翻折,使
向上翻折,使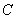 与
与 重合,求线段
重合,求线段
的长。
[番茄花园1]1.
[番茄花园1] 解析:本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。
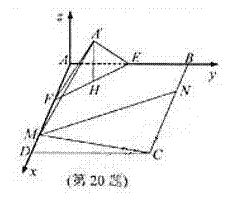 (Ⅰ)解:取线段EF的中点H,连结
(Ⅰ)解:取线段EF的中点H,连结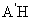 ,因为
,因为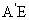 =
=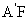 及H是EF的中点,所以
及H是EF的中点,所以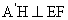 ,
,
又因为平面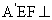 平面
平面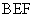 .
.
如图建立空间直角坐标系A-xyz
则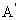 (2,2,
(2,2,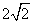 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故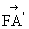 =(-2,2,2
=(-2,2,2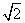 ),
),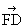 =(6,0,0).
=(6,0,0).
设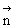 =(x,y,z)为平面
=(x,y,z)为平面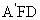 的一个法向量,
的一个法向量,
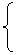 -2x+2y+2
-2x+2y+2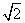 z=0
z=0
所以
6x=0.
取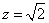 ,则
,则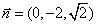 。
。
又平面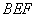 的一个法向量
的一个法向量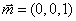 ,
,
故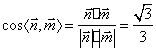 。
。
所以二面角的余弦值为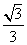
(Ⅱ)解:设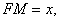 则
则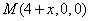 ,
,
因为翻折后,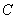 与
与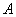 重合,所以
重合,所以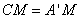 ,
,
故, 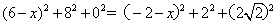 ,得
,得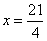 ,
,
经检验,此时点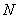 在线段
在线段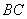 上,
上,
所以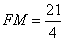 。
。
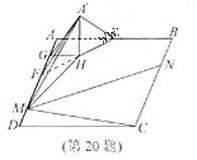 方法二:
方法二:
(Ⅰ)解:取线段 的中点
的中点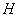 ,
,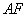 的中点
的中点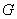 ,连结
,连结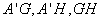 。
。
因为 =
=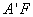 及
及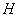 是
是 的中点,
的中点,
所以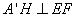
又因为平面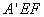
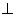 平面
平面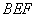 ,
,
所以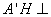 平面
平面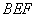 ,
,
又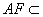 平面
平面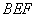 ,
,
故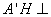
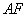 ,
,
又因为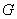 、
、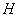 是
是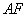 、
、 的中点,
的中点,
易知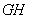 ∥
∥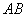 ,
,
所以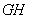
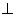
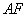 ,
,
于是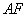
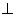 面
面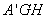 ,
,
所以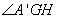 为二面角
为二面角 的平面角,
的平面角,
在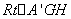 中,
中,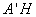 =
=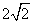 ,
,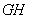 =2,
=2,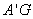 =
=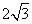
所以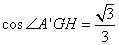 .
.
故二面角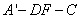 的余弦值为
的余弦值为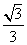 。
。
(Ⅱ)解:设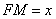 ,
,
因为翻折后,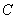 与
与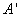 重合,
重合,
所以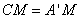 ,
,
而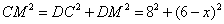 ,
,
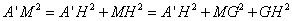
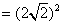
得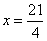 ,
,
经检验,此时点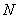 在线段
在线段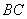 上,
上,
所以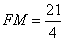 。
。
[番茄花园1]20.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com