
【题目】某市居民自来水收费标准如下:每户每月用水不超过5吨时,每吨为2.6元,当用水超过5吨时,超过部分每吨4元,某月甲、乙两户共交水费y元,已知甲、乙两户该月用水量分别为5x,3x吨.
(1)求y关于x的函数;
(2)若甲、乙两户该月共交水费34.7元,分别求甲、乙两户该月的用水量和水费.
【答案】
(1)解:由题意知,x≥0,令5x=5,得x=1;令3x=5,得x= ![]() .
.
则当0≤x≤1时,
y=(5x+3x)×2.6=20.8x
当1<x≤ ![]() 时,
时,
y=5×2.6+(5x﹣5)×4+3x×2.6=27.8x﹣7,
当x> ![]() 时,
时,
y=(5+5)×2.6+(5x+3x﹣5﹣5)×4=32x﹣14;
即得y= 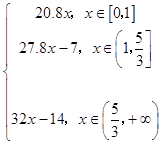
(2)解:由于y=f(x)在各段区间上均单增,
当x∈[0,1]时,y≤f(1)=20.8<34.7;
当x∈(1, ![]() ]时,y≤f(
]时,y≤f( ![]() )≈39.3>34.7;
)≈39.3>34.7;
令27.8x﹣7=34.7,得x=1.5,
所以甲户用水量为5x=7.5吨,付费S1=5×2.6+2.5×4=23元
乙户用水量为3x=4.5吨,付费S2=4.5×2.6=11.7元
【解析】(1)由题意知:x≥0,令5x=5,得x=1;令3x=5,得x= ![]() .将x取值范围分三段,求对应函数解析式可得答案.(2)在分段函数各定义域上讨论函数值对应的x的值
.将x取值范围分三段,求对应函数解析式可得答案.(2)在分段函数各定义域上讨论函数值对应的x的值


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB=AC=5,BB1=BC=6,D,E分别是AA1和B1C的中点 
(1)求证:DE∥平面ABC;
(2)求三棱锥E﹣BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中有5个大小形状完全相同的小球,其中黑色小球有3个,标号分别为1,2,3,白色小球有2个,标号分别为1,2.
(1)若从盒中任取两个小球,求取出的小球颜色相同且标号之和小于或等于4的概率;
(2)若盒子里再放入一个标号为4的红色小球,从中任取两个小球,求取出的两个小球颜色不同且标号之和大于3的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S﹣ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC、SC于D、E,又SA=AB,SB=BC, 
(1)求证:BD⊥平面SAC;
(2)求二面角E﹣BD﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].已知图中x=0.018,则由直观图估算出中位数(精确到0.1)的值为( ) 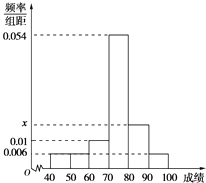
A.75.5
B.75.2
C.75.1
D.75.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】样本(x1 , x2…,xn)的平均数为x,样本(y1 , y2 , …,ym)的平均数为 ![]() (
( ![]() ≠
≠ ![]() ).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数
).若样本(x1 , x2…,xn , y1 , y2 , …,ym)的平均数 ![]() =α
=α ![]() +(1﹣α)
+(1﹣α) ![]() ,其中0<α<
,其中0<α< ![]() ,则n,m的大小关系为( )
,则n,m的大小关系为( )
A.n<m
B.n>m
C.n=m
D.不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4 ![]() x的交点为椭圆
x的交点为椭圆 ![]() (a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点.
(a>b>0)的右焦点,且椭圆的长轴长为4,左右顶点分别为A,B,经过椭圆左焦点的直线l与椭圆交于C,D(异于A,B)两点. 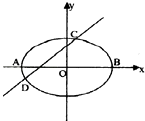
(1)求椭圆标准方程;
(2)求四边形ADBC的面积的最大值;
(3)若M(x1 , y1)N(x2 , y2)是椭圆上的两动点,且满x1x2+2y1y2=0,动点P满足 ![]() (其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
(其中O为坐标原点),是否存在两定点F1 , F2使得|PF1|+|PF2|为定值,若存在求出该定值,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB= ![]() .设线段AB的中点M在l上的投影为N,则
.设线段AB的中点M在l上的投影为N,则 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com