
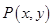 为函数
为函数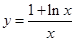 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线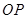 的斜率
的斜率 .
.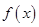 在区间
在区间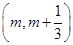
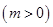 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;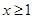 时,不等式
时,不等式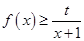 恒成立,求实数
恒成立,求实数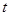 的取值范围;
的取值范围;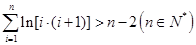 .
.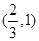 ;(2)
;(2)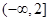 ;(3)详见解析.
;(3)详见解析.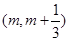 内;(2)首先根据条件分离出变量
内;(2)首先根据条件分离出变量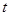 ,由
,由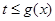 转化成求
转化成求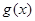 的最小值(利用二次求导判单调性);(3)结合第(2)问构造出含
的最小值(利用二次求导判单调性);(3)结合第(2)问构造出含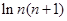
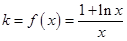 ,
,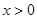 1分
1分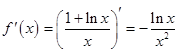 2分
2分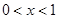 时,
时,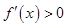 ;当
;当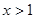 时,
时,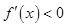 .
. 在
在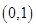 上单调递增,在
上单调递增,在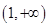 上单调递减,
上单调递减, 在
在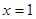 处取得极大值. 3分
处取得极大值. 3分 在区间
在区间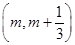 (其中
(其中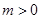 )上存在极值,
)上存在极值,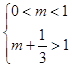 ,得
,得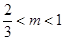 .即实数
.即实数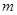 的取值范围是
的取值范围是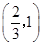 . 4分
. 4分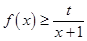 得
得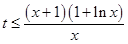 ,令
,令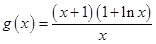 ,
,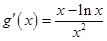 . 6分
. 6分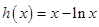 ,则
,则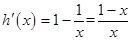 ,
,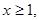 所以
所以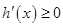 ,故
,故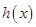 在
在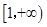 上单调递增. 7分
上单调递增. 7分 ,从而
,从而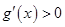
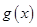 在
在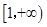 上单调递增,
上单调递增, 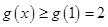
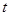 的取值范围是
的取值范围是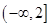 . 9分
. 9分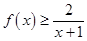 恒成立,
恒成立,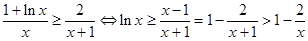 11分
11分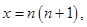 则
则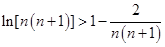 , 12分
, 12分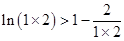 ,
, 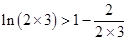 , ,
, ,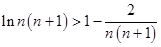 .
.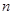 个式子相加得:
个式子相加得: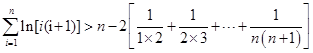
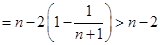 ,
,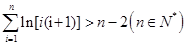 . 14分
. 14分

 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com