
若a=(cosa ,sina ),b=(cosb ,sinb ),
且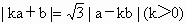 .
.
(1)用k表示数量积a·b.
(2)求a·b的最小值,并求出此时a与b的夹角q .
|
解: (1)由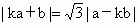 得 得
∴ ∴ ∵|a|=1,|b|=1, ∴ ∴ 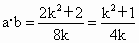 . .
(2) 由函数单调性的定义容易证明
∴当k=1时,
由已知a=(cosa ,sina ),b=(cosb ,sinb ),易知|a|=1,|b|=1,又告诉了有关模的一个等式,我们知道,在研究向量的模的时候是常常将之平方,平方之后将会出现a·b,而第(1)问恰恰就是求a·b,则问题迎刃而解. |
|
本题是一道非常典型的综合题,考查了向量数量积的定义、模长公式、夹角公式,研究向量模的常用方法 (将之平方),运用函数单调性求函数最值. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| 4 |
| 5 |
| BC |
| BA |
查看答案和解析>>
科目:高中数学 来源: 题型:
sin(2π-α)cos(π+α)cos(
| ||||
2sin(3π+α)sin(-π-α)sin(
|
| 25 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分)本题共有3个小题,第1小题满分3分,第2小题满分6分,第3小题满分9分.
已知椭圆![]() 的方程为
的方程为![]() ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).
(1)若直角坐标平面上的点M、A(0,-b),B(a,0)满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,交直线
两点,交直线![]() 于点
于点![]() .若
.若![]() ,证明:
,证明:![]() 为
为![]() 的中点;
的中点;
(3)对于椭圆![]() 上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆
上的点Q(a cosθ,b sinθ)(0<θ<π),如果椭圆![]() 上存在不同的两个交点
上存在不同的两个交点![]() 、
、![]() 满足
满足![]() ,写出求作点
,写出求作点![]() 、
、![]() 的步骤,并求出使
的步骤,并求出使![]() 、
、![]() 存在的θ的取值范围.
存在的θ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com