
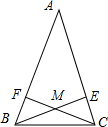
 用分析法和综合法分别证明下题:
用分析法和综合法分别证明下题:分析 综合法证明的特点是“由因导果”,分析法证明的特点是“执果索因”.
解答 证明:(综合法)∵AB=AC,
∴∠ABC=∠ACB,
∵BE⊥AC,CF⊥AB,
∴∠BFC=∠CEB,
∵BC=CB,
∴△BEC≌△CFB,
∴BF=CE,
∵∠BFC=∠CEB,∠BMF=∠CME,
∴△BMF≌△CME,
∴MB=MC.
(分析法)要证明:MB=MC,
只要证明:△BMF≌△CME,
只要证明:BF=CE,∠BFC=∠CEB,∠BMF=∠CME,
只要证明:△BEC≌△CFB,
只要证明:∠ABC=∠ACB,∠BFC=∠CEB,BC=CB,
由AB=AC,BE⊥AC,CF⊥AB,可得.
点评 本题考查综合法与分析法的特点及应用,熟练掌握综合法与分析法是解决问题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com