Question

7．设点P在平面ABC内，若tanA•$\overrightarrow{PA}$+tanB•$\overrightarrow{PB}$+tanC•$\overrightarrow{PC}$=$\overrightarrow{0}$，则点P是△ABC的垂心．

Answer 1

分析 分△ABC为非直角三角形、直角三角形两种情况考虑．

解答 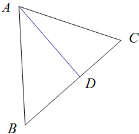解：分△ABC为非直角三角形、直角三角形两种情况考虑：
①当△ABC为非直角三角形时，
如图，过点A作AD⊥BC交于点D，
计边BC的长度为a，边AC的长度为b，边AB的长度为c．
由tanA•$\overrightarrow{PA}$+tanB•$\overrightarrow{PB}$+tanC•$\overrightarrow{PC}$=$\overrightarrow{0}$变形，
得$（tanA+tanB+tanC）•\overrightarrow{AP}=tanB•\overrightarrow{AB}+tanC•\overrightarrow{AC}$，
即$\overrightarrow{AP}=\frac{tanB}{tanA+tanB+tanC}•\overrightarrow{AB}+\frac{tanC}{tanA+tanB+tanC}$•$\overrightarrow{AC}$，
由于$\overrightarrow{AD}=\frac{1}{1+\frac{ccosB}{bcosC}}\overrightarrow{AB}$+$\frac{\frac{ccosB}{bcosC}}{1+\frac{ccosB}{bcosC}}\overrightarrow{AC}$
=$\frac{bcosC}{bcosC+ccosB}\overrightarrow{AB}$+$\frac{ccosB}{bcosC+ccosB}\overrightarrow{AC}$
由正弦定理，得：a=2RsinA，b=2RsinB，c=2RsinC，
上式化为$\frac{sinBcosC}{sinBcosC+sinCcosB}\overrightarrow{AB}$+$\frac{sinCcosB}{sinBcosC+sinCcosB}\overrightarrow{AC}$
=$\frac{sinBcosC}{sinA}\overrightarrow{AB}$+$\frac{sinCcosB}{sinA}\overrightarrow{AC}$，
而$\frac{\frac{tanC}{tanA+tanB+tanC}}{\frac{sinCcosB}{sinA}}$=$\frac{sinA}{（tanA+tanB+tanC）cosBcosC}$，
$\frac{\frac{tanB}{tanA+tanB+tanC}}{\frac{sinBcosC}{sinA}}$=$\frac{sinA}{（tanA+tanB+tanC）cosBcosC}$，
所以$\overrightarrow{AP}$与$\overrightarrow{AD}$共线，即点P在BC边的高线上；
同理，点P也在CA、AB边的高线上，
从而P为△ABC的垂心．
②当△ABC为非直角三角形时，
若A为直角时，点A即为三角形的垂心；
对B和C为直角时，同理可得．
综上，点P是△ABC的垂心．

点评 本题考查三角形垂心的向量表示，运用到了向量的一些性质、正弦定理等知识，本题中的结论和条件互换也成立，属难题．