
【题目】已知函数f(x)为偶函数,当x<0时,f(x)=ln(﹣x)﹣ax.若直线y=x与曲线y=f(x)至少有两个交点,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:设x>0,则﹣x<0,
∵f(x)为偶函数,且当x<0时,f(x)=ln(﹣x)﹣ax,
∴当x>0时,f(x)=f(﹣x)=lnx+ax.
∴f(x)= ![]() .
.
若直线y=x与曲线y=f(x)至少有两个交点,即方程f(x)=x至少有两个根.
令g(x)=f(x)﹣x= ![]() .
.
下面研究:
当x<0时,函数g(x)=ln(﹣x)﹣ax﹣x零点情况:
由g(x)=ln(﹣x)﹣ax﹣x=0,得ln(﹣x)=(a+1)x.
作出y=ln(﹣x)的图象如图:

若a+1≥0,即a≥﹣1,则y=ln(﹣x)与y=(a+1)x有1个交点,
若a+1<0,即a<﹣1,设直线y=(a+1)x与y=ln(﹣x)的切点为(x0,ln(﹣x0)),
则切线方程为y﹣ln(﹣x0)= ![]() (x﹣x0),代入原点(0,0),可得ln(﹣x0)=1,x0=﹣e.
(x﹣x0),代入原点(0,0),可得ln(﹣x0)=1,x0=﹣e.
则切点为(﹣e,1),切线斜率为﹣ ![]() ,要使直线y=(a+1)x与y=ln(﹣x)有交点,则a+1
,要使直线y=(a+1)x与y=ln(﹣x)有交点,则a+1 ![]() ,即a
,即a ![]() ;
;
当x>0时,函数g(x)=lnx+ax﹣x零点情况:
由g(x)=lnx+ax﹣x=0,得lnx=(﹣a+1)x.
作出y=lnx的图象如图:

若﹣a+1≤0,即a≥1,则y=lnx与y=(﹣a+1)x有1个交点,
若﹣a+1>0,即a<1,设直线y=(﹣a+1)x与y=lnx的切点为(x0,lnx0),
则切线方程为y﹣lnx0= ![]() (x﹣x0),代入原点(0,0),可得lnx0=1,x0=e.
(x﹣x0),代入原点(0,0),可得lnx0=1,x0=e.
则切点为(e,1),切线斜率为 ![]() ,要使直线y=(﹣a+1)x与y=lnx有交点,则﹣a+1
,要使直线y=(﹣a+1)x与y=lnx有交点,则﹣a+1 ![]() ,即
,即 ![]() .
.
综上,满足直线y=x与曲线y=f(x)至少有两个交点,则实数a的取值范围是 ![]() .
.
故选:D.


科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图. 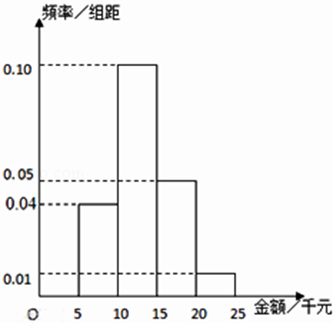
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l在直角坐标系xOy中的参数方程为 ![]() 为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)写出曲线C的直角坐标方程;
(2)点Q(a,0),若直线l与曲线C交于A、B两点,求使 ![]() 为定值的值.
为定值的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,F,A,B 分别为椭圆 ![]() 的右焦点、右顶点和上顶点,若
的右焦点、右顶点和上顶点,若 ![]()
(1)求a的值;
(2)过点P(0,2)作直线l 交椭圆于M,N 两点,过M 作平行于x 轴的直线交椭圆于另外一点Q,连接NQ ,求证:直线NQ 经过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在自然数列1,2,3,,n中,任取k个元素位置保持不动,将其余n﹣k个元素变动位置,得到不同的新数列.由此产生的不同新数列的个数记为Pn(k).
(1)求P3(1)
(2)求 ![]() P4(k);
P4(k);
(3)证明 ![]() kPn(k)=n
kPn(k)=n ![]() Pn﹣1(k),并求出
Pn﹣1(k),并求出 ![]() kPn(k)的值.
kPn(k)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出n瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这n瓶酒,并重新按品质优劣为它们排序,这称为一轮测试.根据一轮测试中的两次排序的偏离程度的高低为其评分. 现设n=4,分别以a1 , a2 , a3 , a4表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令X=|1﹣a1|+|2﹣a2|+|3﹣a3|+|4﹣a4|,
则X是对两次排序的偏离程度的一种描述.
(Ⅰ)写出X的可能值集合;
(Ⅱ)假设a1 , a2 , a3 , a4等可能地为1,2,3,4的各种排列,求X的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有X≤2,
①试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);②你认为该品酒师的酒味鉴别功能如何?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定:点P(x,y)按向量 ![]() 平移后的点为Q(x+a,y+b).若函数
平移后的点为Q(x+a,y+b).若函数 ![]() 的图象按向量
的图象按向量 ![]() =(j,k)且|j|
=(j,k)且|j| ![]() 平移后的图象对应的函数是
平移后的图象对应的函数是 ![]() +1.
+1.
(1)试求向量 ![]() 的坐标;
的坐标;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,已知f(2A)+2cos(B+C)=1, ①求角A的大小;
②若a=6,求b+c的取值范围.
另外:最后一小题也可用“余弦定理结合基本不等式”求解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com