若三点A(3,3)、B(a,0)、C(0,b)(ab≠0)共线,则 .
【答案】
分析:利用向量的坐标公式:终点坐标减去始点坐标,求出向量的坐标;据三点共线则它们确定的向量共线,利用向量共线的充要条件列出方程得到a,b的关系.
解答:解:∵点A(3,3)、B(a,0)、C(0,b)(ab≠0)
∴
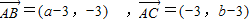
∵点A(3,3)、B(a,0)、C(0,b)(ab≠0)共线
∴
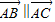
∴(a-3)×(b-3)=-3×(-3)
所以ab-3a-3b=0
故答案为:ab-3a-3b=0
点评:本题考查利用点的坐标求向量的坐标、向量共线的充要条件、向量共线与三点共线的关系.
