
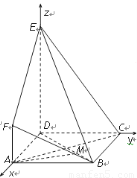
如图, 是边长为
是边长为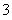 的正方形,
的正方形,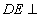 平面
平面 ,
,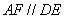 ,
,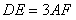 ,
,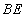 与平面
与平面 所成角为
所成角为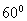 .
.
(1)求证: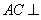 平面
平面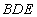 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)设点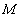 是线段
是线段 上一个动点,试确定点
上一个动点,试确定点 的位置,使得
的位置,使得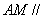 平面
平面 ,并证明你的结论.
,并证明你的结论.
(1) 参考解析;(2) 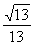 ; (3)
; (3) 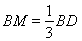
【解析】
试题分析:(1)因为要证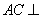 平面
平面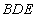 即直线与平面垂直的证明,通过证明这条直线垂直平面内的两条相交直线即可,依题意易得到.
即直线与平面垂直的证明,通过证明这条直线垂直平面内的两条相交直线即可,依题意易得到.
(2)因为要求二面角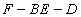 的余弦值,一般是通过建立空间坐标系,写出相应的点的坐标,由于AC所在的向量就是平面EDB的法向量,所以关键是通过待定系数法求出平面EFB的法向量.再通过两法向量的夹角得到两平面的二面角的大小,二面角是钝角还是锐角通过图形来确定.
的余弦值,一般是通过建立空间坐标系,写出相应的点的坐标,由于AC所在的向量就是平面EDB的法向量,所以关键是通过待定系数法求出平面EFB的法向量.再通过两法向量的夹角得到两平面的二面角的大小,二面角是钝角还是锐角通过图形来确定.
(3)因为点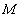 是线段
是线段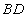 上一个动点,试确定点
上一个动点,试确定点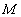 的位置,使得
的位置,使得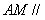 平面
平面 .通过对点M的假设写出向量AM.从而由该向量垂直平面的法向量,即可得到相应的点M的坐标.
.通过对点M的假设写出向量AM.从而由该向量垂直平面的法向量,即可得到相应的点M的坐标.
试题解析:(1)证明: 因为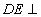 平面
平面 , 所以
, 所以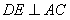 .
.
因为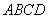 是正方形,所以
是正方形,所以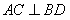 ,又
,又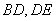 相交
相交
从而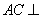 平面
平面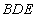 .
.
(2)解:因为 两两垂直,所以建立空间直角坐标系
两两垂直,所以建立空间直角坐标系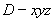 如图所示.因为
如图所示.因为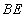 与平面
与平面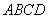 所成角为
所成角为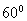 , 即
, 即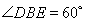 ,
,
所以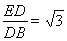 .由
.由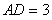 可知
可知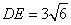 ,
,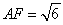 .
.
则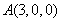 ,
,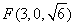 ,
,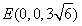 ,
,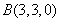 ,
,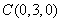 ,
,
所以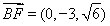 ,
,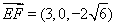 ,
,
设平面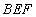 的法向量为
的法向量为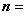
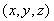 ,则
,则 ,即
,即 ,
,
令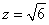 ,则
,则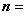
 . 因为
. 因为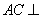 平面
平面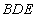 ,所以
,所以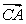 为平面
为平面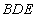 的法向量,
的法向量,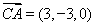 ,
,
所以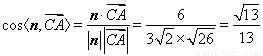 .
.
因为二面角为锐角,所以二面角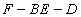 的余弦值为
的余弦值为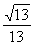 .
.
(3)解:点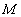 是线段
是线段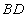 上一个动点,设
上一个动点,设 . 则
. 则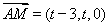 ,
,
因为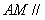 平面
平面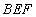 ,所以
,所以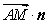
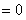 ,
,
即 ,解得
,解得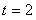 .
.
此时,点 坐标为
坐标为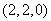 ,
,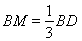 ,符合题意.
,符合题意.
考点:1.线面垂直的证明.2.二面角的问题.3.直线与平面平行.4.空间想象能力.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
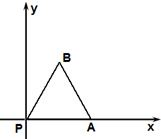 如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是
如图放置的边长为1的正三角形PAB沿x轴滚动,设顶点A(x,y)的纵坐标与横坐标的函数关系式是y=f(x),则f(x)在区间[-2,1]上的解析式是查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省、华师附中、深圳中学、广雅中学高三上学期期末数学理卷 题型:填空题
如图放置的边长为 的正三角形
的正三角形 沿
沿 轴滚动,设顶点
轴滚动,设顶点
 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是 ,则
,则 在区间
在区间 上的解析式是 ;(说明:“正三角形
上的解析式是 ;(说明:“正三角形 沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形
沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形 也可以沿x轴负方向逆时针滚动)
也可以沿x轴负方向逆时针滚动)

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省、华师附中、深圳中学、广雅中学高三上学期期末数学理卷 题型:填空题
如图放置的边长为 的正三角形
的正三角形 沿
沿 轴滚动,设顶点
轴滚动,设顶点
 的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是 ,则
,则 在区间
在区间 上的解析式是 ;(说明:“正三角形
上的解析式是 ;(说明:“正三角形 沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形
沿x轴滚动”包括沿x轴正方向和沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形 也可以沿x轴负方向逆时针滚动)
也可以沿x轴负方向逆时针滚动)

查看答案和解析>>
科目:高中数学 来源:2011届广东省实验中学、华师附中、深圳中学、广雅中学高三上学期期末数学理卷 题型:填空题
如图放置的边长为 的正三角形
的正三角形 沿
沿 轴滚动,设顶点
轴滚动,设顶点  的纵坐标与横坐标的函数关系式是
的纵坐标与横坐标的函数关系式是 ,则
,则 在区间
在区间 上的解析式是 ;(说明:“正三角形
上的解析式是 ;(说明:“正三角形 沿x轴滚动”包括沿x轴正方向和
沿x轴滚动”包括沿x轴正方向和 沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形
沿x轴负方向滚动.沿x轴正方向滚动指的是先以顶点A为中心顺时针旋转,当顶点B落在x轴上时,再以顶点B为中心顺时针旋转,如此继续.;类似地,正三角形 也可以沿x轴负方向逆时针滚动)
也可以沿x轴负方向逆时针滚动)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com