
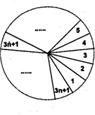
 一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P
一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P <p≤
<p≤
 ,
, ]内的定值
]内的定值 ≤p<
≤p<
 ,
, )内的定值
)内的定值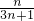 ,
,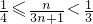
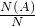 求解.
求解. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
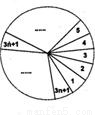
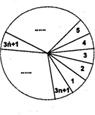 一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P( )
一只质地均匀的圆形转盘,按如图所示的方法等分成3n+1(n∈n0)个区域,并且将各区域分别标上1,2,3,…,3n+1中的一个数字(不重复)作为区域的代号.任意转动转盘,当转盘停止时,如果指针不恰好指向区域的边界,则指针所指区域的代号属于集合{4,7,10,…,3n+1)的概率P( )A、随着n值的增大而减小且
| ||||
B、是一个与n无关且落在区间(
| ||||
C、随着n值的增大而增大且
| ||||
D、是一个与n无关且落在区间,[
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•泰州三模)如图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的
(2013•泰州三模)如图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的| 1 |
| 12 |
| 1 |
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省五市高三第三次调研测试数学试卷(解析版) 题型:解答题
下图是某游戏中使用的材质均匀的圆形转盘,其中Ⅰ,Ⅱ,Ⅲ,Ⅳ部分的面积各占转盘面积的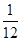 ,
,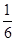 ,
,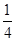 ,
,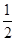 .游戏规则如下:
.游戏规则如下:
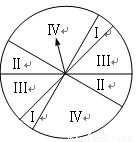
① 当指针指到Ⅰ,Ⅱ, Ⅲ,Ⅳ部分时,分别获得积分100分,40分,10分,0分;
② (ⅰ)若参加该游戏转一次转盘获得的积分不是40分,则按①获得相应的积分,游戏结束;
(ⅱ)若参加该游戏转一次获得的积分是40分,则用抛一枚质地均匀的硬币的方法来决定是否继续游戏.正面向上时,游戏结束;反面向上时,再转一次转盘,若再转一次的积分不高于40分,则最终积分为0分,否则最终积分为100分,游戏结束.
设某人参加该游戏一次所获积分为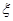 .
.
(1)求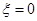 的概率;
的概率;
(2)求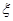 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源:2010年福建省各地市高考数学模拟试卷分类汇编13:概率(解析版) 题型:选择题
 <p≤
<p≤
 ,
, ]内的定值
]内的定值 ≤p<
≤p<
 ,
, )内的定值
)内的定值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com