
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明: ![]() <0.
<0.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,理由见解析
,理由见解析
【解析】试题分析:(1)![]() ,可知
,可知![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2)
,1]是增函数,在[1,2]是减函数,所以最大值为f(1).(2) ![]() 在区间
在区间![]() 上为单调递增函数,即
上为单调递增函数,即![]() 在
在![]() 上恒成立。
上恒成立。![]() ,利用分离参数
,利用分离参数![]() 在
在![]() 上恒成立,即求
上恒成立,即求![]() 的最大值。
的最大值。
(3)![]() 有两个实根
有两个实根![]() ,
, ![]() ,两式相减
,两式相减![]() ,又
,又![]() ,
, ![]()
![]() .要证:
.要证: ![]() ,只需证:
,只需证:![]() ,令
,令![]() 可证。
可证。
试题解析:(1) ![]()
函数![]() 在[
在[![]() ,1]是增函数,在[1,2]是减函数,
,1]是增函数,在[1,2]是减函数,
所以![]() .
.
(2)因为![]() ,所以
,所以![]() ,
,
因为![]() 在区间
在区间![]() 单调递增函数,所以
单调递增函数,所以![]() 在(0,3)恒成立
在(0,3)恒成立
![]() ,有
,有![]() =
=![]() ,(
,(![]() )
)
综上: ![]()
(3)∵![]() ,又
,又![]() 有两个实根
有两个实根![]() ,
,
∴![]() ,两式相减,得
,两式相减,得![]() ,
,
∴![]() ,
,
于是![]()
![]() .
.
![]()
要证: ![]() ,只需证:
,只需证:![]()
只需证:![]() .(*)
.(*)
令![]() ,∴(*)化为
,∴(*)化为 ![]() ,只证
,只证![]() 即可.
即可.
![]() 在(0,1)上单调递增,
在(0,1)上单调递增,![]() ,
,
即![]() .∴
.∴![]() .
.
(其他解法根据情况酌情给分)


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当![]() 不是原点时,定义
不是原点时,定义![]() 的“伴随点”为
的“伴随点”为![]() ;当
;当![]() 是原点时,定义
是原点时,定义![]() 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线![]() 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线![]() 定义为曲线
定义为曲线![]() 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:
①若点![]() 的“伴随点”是点
的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点
的“伴随点”是点![]() ;
;
②若曲线![]() 关于
关于![]() 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” ![]() 关于
关于![]() 轴对称;
轴对称;
③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一数集的任一元素的倒数仍在该集合中,则称该数集为“可倒数集”.
(1)判断集合A={-1,1,2}是否为可倒数集;
(2)试写出一个含3个元素的可倒数集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与市场预测,知A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2.(注:所示图中的横坐标表示投资金额,单位:万元)

图1 图2
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 是过点
是过点![]() ,倾斜角为
,倾斜角为![]() 的直线,以直角坐标系
的直线,以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的一个参数方程;
的一个参数方程;
(2)曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府决定建造一批保障房供给社会,缓解贫困人口的住房问题,计划用1 600万元购得一块土地,在该土地上建造10幢楼房的住宅小区,每幢楼的楼层数相同,且每层建筑面积均为1 000平方米,每平方米的建筑费用与楼层有关,第x层楼房每平方米的建筑费用为(kx+800)元(其中k为常数).经测算,若每幢楼为5层,则该小区每平方米的平均综合费用为1 270元.
注:每平方米平均综合费用=![]() .
.
(1) 求k的值;
(2) 问要使该小区楼房每平方米的平均综合费用最低,应将这10幢楼房建成多少层?此时每平方米的平均综合费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
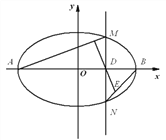
【题目】已知椭圆![]() 的两个顶点分别为
的两个顶点分别为![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为
为![]() 轴上一点,过
轴上一点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 于不同的两点
于不同的两点![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .求
.求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com