
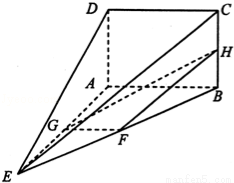
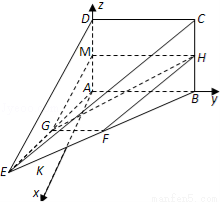
如图,在四棱锥E﹣ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(1)求证:DE∥平面FGH;
(2)若点P在直线GF上, =λ
=λ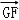 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为 ,求λ的值.
,求λ的值.
(1)证明见解析;(2)λ的值等于1或4.
【解析】
试题分析:(1)取AD的中点M,连接MH,MG,由G、H、F分别是AE、BC、BE的中点,得MH∥GF,G、F、H、M四点共面,又MG∥DE,所以DE∥平面MGFH;(2)在平面ABE内过A作AB的垂线,记为AP,则AP⊥平面ABCD.以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴,建立建立空间直角坐标系A﹣xyz,如图所示.可得 坐标,利用空间向量的坐标运算求出平面PBD的一个法向量=(5﹣2λ,
坐标,利用空间向量的坐标运算求出平面PBD的一个法向量=(5﹣2λ,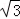 ,2
,2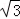 )
)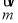 ,再由图可知平面ABP的一个法向量为
,再由图可知平面ABP的一个法向量为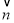 ,由cos<
,由cos<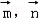 >=
>= =
=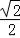 得λ=1或4.
得λ=1或4.
【解析】
(1)证明:取AD的中点M,连接MH,MG.
∵G、H、F分别是AE、BC、BE的中点,
∴MH∥AB,GF∥AB,
∴MH∥GF,即G、F、H、M四点共面,平面FGH即平面MGFH,
又∵△ADE中,MG是中位线,∴MG∥DE
∵DE?平面MGFH,MG?平面MGFH,
∴DE∥平面MGFH,即直线DE与平面FGH平行.
(2)在平面ABE内,过A作AB的垂线,记为AP,则AP⊥平面ABCD.
以A为原点,AP、AB、AD所在的直线分别为x轴,y轴,z轴,
建立建立空间直角坐标系A﹣xyz,如图所示.
可得A(0,0,0),B(0,4,0),D(0,0,2),E(2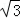 ,﹣2,0),G(
,﹣2,0),G(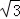 ,﹣1,0),F(
,﹣1,0),F(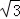 ,1,0)
,1,0)
∴ =(0,2,0),
=(0,2,0),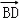 =(0,﹣4,2),
=(0,﹣4,2),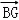 =(
=(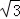 ,﹣5,0).
,﹣5,0).
由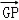 =λ
=λ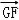 =(0,2λ,0),可得
=(0,2λ,0),可得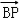 =
= +
+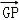 =(
=(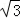 ,2λ﹣5,0).
,2λ﹣5,0).
设平面PBD的法向量为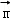 =(x,y,z),
=(x,y,z),
则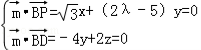 ,取y=
,取y=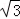 ,得z=2
,得z=2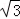 ,x=5﹣2λ,
,x=5﹣2λ,
∴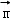 =(5﹣2λ,
=(5﹣2λ,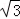 ,2
,2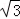 ),
),
又∵平面ABP的一个法向量为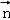 =(0,0,1),
=(0,0,1),
∴cos<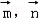 >=
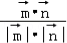
>= =
= =cos
=cos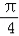 =
=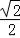 ,解之得λ=1或4
,解之得λ=1或4
即λ的值等于1或4.
考点:1.线面平行的性质与判定;2.二面角;3.空间想象能力.


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源:2015届辽宁省分校高二下学期期末考试文科数学试卷(解析版) 题型:解答题
在四棱锥 中,底面
中,底面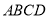 为矩形,
为矩形,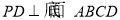 ,
,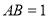 ,
,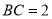 ,
, ,
,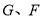 分别为
分别为 的中点.
的中点.
(1) 求证: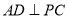 ;
;
(2) 求证: 平面
平面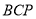 ;
;

查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试理科数学试卷(解析版) 题型:选择题
某一批花生种子,若每1粒发芽的概率为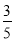 ,则播下3粒种子恰有2粒发芽的概率为( ).
,则播下3粒种子恰有2粒发芽的概率为( ).
A. 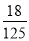 B.
B. 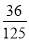 C.
C.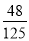 D.
D.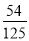
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省大连市五校高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知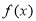 是定义在R上的奇函数,当
是定义在R上的奇函数,当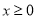 时
时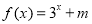 (m为常数),则
(m为常数),则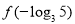 的值为( ).
的值为( ).
A.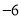 B.6 C.4 D.
B.6 C.4 D.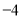
查看答案和解析>>
科目:高中数学 来源:2015届贵州省高二下学期期中理科数学试卷(解析版) 题型:选择题
已知抛物线关于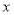 轴对称,它的顶点在坐标原点
轴对称,它的顶点在坐标原点 ,并且经过点
,并且经过点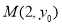 。若点
。若点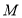 到该抛物线焦点的距离为
到该抛物线焦点的距离为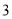 ,则
,则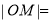 ( )
( )
A、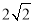 B、
B、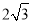 C、
C、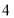 D、
D、
查看答案和解析>>
科目:高中数学 来源:2015届贵州省高二下学期期中文科数学试卷(解析版) 题型:填空题
已知x与y之间的一组数据如下,则y与x的线性回归方程为y=bx+a,必过点 .
x | 1 | 1 | 2 | 4 |
y | 1 | 4 | 5 | 6 |
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标3章练习卷(解析版) 题型:填空题
某单位为了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温.
气温(℃) | 14 | 12 | 8 | 6 |
用电量(度) | 22 | 26 | 34 | 38 |
由表中数据得线性回归方程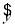 =
=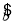 x+
x+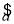 中
中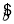 =-2,据此预测当气温为5 ℃时,用电量的度数约为________.
=-2,据此预测当气温为5 ℃时,用电量的度数约为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com