
 和
和 ,甲、乙两人各射击一次,有下列说法:
,甲、乙两人各射击一次,有下列说法: ;
; ;
;  ;
;  .
. ,故①错;
,故①错;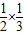 ,故②正确;
,故②正确; ,故③错;
,故③错;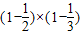 =
= ,则目标被命中的概率为1-
,则目标被命中的概率为1- ,故④正确.
,故④正确. 也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B).
也相互独立,②若A,B相互独立,则P(AB)=P(A)•P(B). 

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2014届海南琼海高二下学期教学质量监测理科数学试卷(解析版) 题型:选择题
甲、乙两人练习射击, 命中目标的概率分别为 和
和 , 甲、乙两人各射击一次,目标被命中的概率为:
, 甲、乙两人各射击一次,目标被命中的概率为:
A. B.
B. C.
C.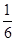 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期期末理科数学试卷(解析版) 题型:选择题
.甲、乙两人练习射击, 命中目标的概率分别为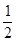 和
和 , 甲、乙两人各射击一次,有下列说法: ①
目标恰好被命中一次的概率为
, 甲、乙两人各射击一次,有下列说法: ①
目标恰好被命中一次的概率为 ;② 目标恰好被命中两次的概率为
;② 目标恰好被命中两次的概率为 ;
③ 目标被命中的概率为
;
③ 目标被命中的概率为 ; ④ 目标被命中的概率为
; ④ 目标被命中的概率为  。以上说法正确的序号依次是
。以上说法正确的序号依次是
A.②③ B.①②③ C.②④ D.①③
查看答案和解析>>
科目:高中数学 来源:《概率》2013年高三数学一轮复习单元训练(浙江大学附中)(解析版) 题型:选择题
 和
和 ,甲、乙两人各射击一次,有下列说法:
,甲、乙两人各射击一次,有下列说法: ;
; ;
;  ;
;  .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com