

 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,再以C为圆心,旋转90°,这时候以CP为半径,因此最终构成图象如下:
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BP为半径,旋转90°,再以C为圆心,旋转90°,这时候以CP为半径,因此最终构成图象如下: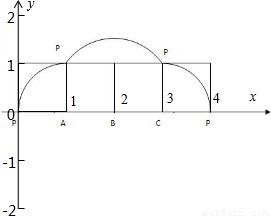
 ×π+2×
×π+2× ×1×1+
×1×1+ ×2π=π+1
×2π=π+1

科目:高中数学 来源: 题型:
 如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=
如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=查看答案和解析>>
科目:高中数学 来源:北京高考真题 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com