练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数f(x)是R上的增函数，设F(x)=f(x)-f(a-x).

    (1)用函数单调性定义证明F(x)是R上的增函数；

    (2)求证：函数y=F(x)的图像关于点(,0)成中心对称图形.

    思路分析：(1)证明函数F(x)的单调性要用到函数f(x)的单调性；(2)证明函数y=F(x)的图像上任一点关于点(,0)的对称点也在函数y=F(x)图像上即可.

    解：(1)设x1、x2∈R，且x1＜x2，则

    F(x1)-F(x2)=［f(x1)-f(a-x1)］-［f(x2)-f(a-x2)］

    =［f(x1)-f(x2)］+［f(a-x2)-(a-x1)］.

    又∵函数f(x)是R上的增函数，x1＜x2，

    ∴a-x2＜a-x1.

    ∴f(x1)＜f(x2).∴f(a-x2)＜f(a-x1).

    ∴［f(x1)-f(x2)］+［f(a-x2)-f(a-x1)］＜0.

    ∴F(x1)＜F(x2).

    ∴F(x)是R上的增函数.

    (2)设点M(x0,F(x0))是函数F(x)图像上任意一点，则点M(x0,F(x0))关于点(,0)的对称点M′(a-x0,-F(x0)).

    又∵F(a-x0)=f(a-x0)-f［a-(a-x0)］

    =f(a-x0)-f(x0)

    =-［f(x0)-f(a-x0)］

    =-F(x0),

    ∴点M′(a-x0,-F(x0))也在函数F(x)图像上.

    又∵点M(x0,F(x0))是函数F(x)图像上任意一点，

    ∴函数y=F(x)的图像关于点(,0)成中心对称图形.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)是R上的增函数,a、b∈R.

    (1)证明命题“如果a+b≥0,那么f(a)+f(b)≥f(-a)+f(-b)成立”;

    (2)判断(1)中命题的逆命题是否成立,并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)是R上的偶函数,g(x)是R上的奇函数,且g(x)=f(x-1),若f(2)=2,则f(2 006)的值为(    )

    A.2            B.0            C.-2            D.±2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)是R上的增函数，A（0，-1）、B（3，1）是其图象上的两点，那么|f(x+1)|＜1的解集是(    )

    A.（1，4）                                B.（-1，2）

    C.（-∞,1]∪［4,+∞)                  D.(-∞,-1］∪［2,+∞)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)是R上的奇函数，f(1)=m，f(3)=n，m+n＞0，则(    )

    A．f(3)＞f(-1)                           B．f(3)＜f(-1)

    C．f(3)=f(-1)                            D．f(3)与f(-1)的大小无法确定

    查看答案和解析>>

    科目：高中数学 来源：2014届黑龙江省高一期末考试文科数学 题型：选择题

    已知函数f(X)是R上的增函数, A(0,-1) ，B（3，1）是其图象上的两点，那么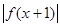＜1的解集的补集是（     ）

        A．（-1，2）  B.(1, 4)  C.(-∞,－1)∪〔4, +∞)    D. (-∞,－1〕∪〔2, +∞)

     

    查看答案和解析>>

    同步练习册答案