
在一个花瓶中装有6枝鲜花,其中3枝山茶花,2枝杜鹃花和1枝君子兰,从中任取2枝鲜花.
(1)求恰有一枝山茶花的概率;
(2)求没有君子兰的概率.
(1)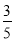 ;(2)
;(2) .
.
【解析】
试题分析:本题是古典概型的概率计算问题,古典概型的概率计算,关键是计算出基本事件总数,某个事件发生时所包含的基本事件数,然后代入公式即可求解,本题采用列举法找出从6枝鲜花中任取2枝鲜花的所有可能有15种,对于(1)“恰有一枝山茶花”事件包含了9种基本事件,对于(2)“没有君子兰”事件则包含了10种基本事件,然后按照古典概率的计算公式进行计算即可.
试题解析:设3枝山茶花为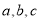 ,2枝杜鹃花为
,2枝杜鹃花为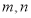 ,1枝君子兰为
,1枝君子兰为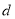 . 则从6枝鲜花中任取2枝的基本事件有:
. 则从6枝鲜花中任取2枝的基本事件有: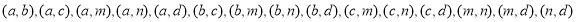 , 共15种 4分
, 共15种 4分
(1)其中恰有一枝山茶花的基本事件有: 共9种,所以恰有一枝山茶花的概率为
共9种,所以恰有一枝山茶花的概率为 8分
8分
(2)其中没有君子兰的基本事件有: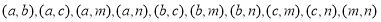 共10种,所以没有君子兰的概率为
共10种,所以没有君子兰的概率为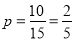 12分.
12分.
考点:古典概型的概率计算.


科目:高中数学 来源:2015届安徽蚌埠高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
点B是点A(1,2,3)在坐标平面 内的射影,则OB等于( )
内的射影,则OB等于( )
A.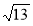 B.
B. C.
C.  D.
D.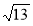
查看答案和解析>>
科目:高中数学 来源:2015届四川资阳市高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示,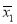 ,
,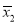 分别表示甲、乙两名运动员这项测试成绩的平均数,
分别表示甲、乙两名运动员这项测试成绩的平均数,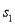 ,
, 分别表示甲、乙两名运动员这项测试成绩的标准差,则有( )
分别表示甲、乙两名运动员这项测试成绩的标准差,则有( )

A.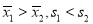 B.
B. C.
C.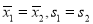 D.
D.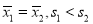
查看答案和解析>>
科目:高中数学 来源:2015届四川资阳市高二第一学期期末考试文科数学试卷(解析版) 题型:解答题
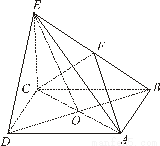
在四棱锥 中,底面
中,底面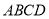 是正方形,
是正方形,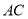 与
与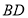 交于点
交于点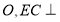 底面
底面 ,
, 为
为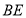 的中点.
的中点.
(1)求证: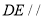 平面
平面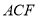 ;
;
(2)若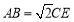 ,在线段
,在线段 上是否存在点
上是否存在点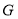 ,使
,使 平面
平面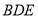 ?若存在,求出
?若存在,求出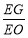 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届四川资阳市高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
10名工人某天生产同一种零件,生产的件数是15,17,14,10,15,17,17,16,14,12;设其平均数为 ,中位数为
,中位数为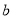 ,众数为
,众数为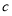 ,则有( )
,则有( )
A.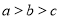 B.
B.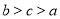 C.
C.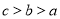 D.
D.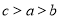
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高二上学期期末理数学试卷(解析版) 题型:选择题
在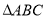 中,
中,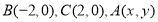 ,给出
,给出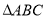 满足的条件,就能得到动点
满足的条件,就能得到动点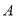 的轨迹方程,下表给出了一些条件及方程:
的轨迹方程,下表给出了一些条件及方程:
条件 | 方程 |
① |
|
② |
|
③ |
|
则满足条件①、②、③的点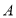 轨迹方程按顺序分别是
轨迹方程按顺序分别是
A. 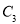 、
、 、
、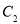 B.
B. 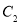 、
、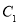 、
、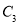
C. 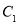 、
、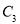 、
、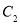 D.
D. 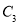 、
、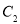 、
、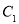
查看答案和解析>>
科目:高中数学 来源:2015届北京海淀区高二上学期期末考试理科数学试卷(解析版) 题型:选择题
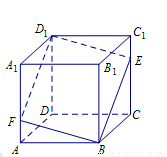
如图所示,在正方体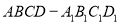 中,点
中,点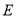 是棱
是棱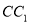 上的一个动点,平面
上的一个动点,平面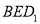 交棱
交棱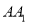 于点
于点 .则下列命题中假命题是( )
.则下列命题中假命题是( )
(A)存在点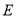 ,使得
,使得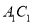 //平面
//平面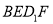
(B)存在点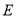 ,使得
,使得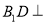 平面
平面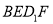
(C)对于任意的点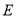 ,平面
,平面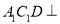 平面
平面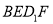
(D)对于任意的点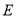 ,四棱锥
,四棱锥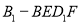 的体积均不变
的体积均不变
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com