
【题目】已知函数![]() 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列
的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列![]() 的前n项和Sn=f(n)(n∈N*).
的前n项和Sn=f(n)(n∈N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列{![]() }前n项的和Tn.
}前n项的和Tn.
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱台![]() 中,点
中,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 是
是![]() 内(含边界)的一个动点,且有平面
内(含边界)的一个动点,且有平面![]() 平面
平面![]() ,则动点
,则动点![]() 的轨迹是( )
的轨迹是( )

A. 平面B. 直线C. 线段,但只含1个端点D. 圆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S-ABC中,∠ABC=90°,D是AC的中点,且SA=SB=SC.
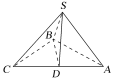
(1)求证:SD⊥平面ABC;
(2)若AB=BC,求证:BD⊥平面SAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆台的上、下底面半径分别为![]() 、
、![]() ,母线长
,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点(
点(![]() 在下底面),求:
在下底面),求:
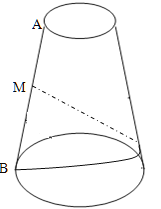
(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱![]() 的侧棱垂直于底面,
的侧棱垂直于底面,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 的中点.
的中点.

(1)若![]() ,求三棱柱
,求三棱柱![]() 的体积;
的体积;
(2)证明:![]() 平面
平面![]() ;
;
(3)请问当![]() 为何值时,
为何值时,![]() 平面
平面![]() ,试证明你的结论.
,试证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=![]() (n∈N*)
(n∈N*)
(Ⅰ)证明当n≥2时,数列{nan}是等比数列,并求数列{an}的通项an;
(Ⅱ)求数列{n2an}的前n项和Tn;
(Ⅲ)对任意n∈N*,使得![]() 恒成立,求实数λ的最小值.
恒成立,求实数λ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com