练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    集合A＝｛1，2｝的真子集的个数是（    ）．

    A．1 B．2 C．3 D．4 

    C

    解析试题分析：因为集合A＝｛1，2｝有2个元素，所以真子集的个数为。
    考点：子集；真子集。
    点评：熟记公式：若集合中有n个元素，则它有个子集，有个非空子集，有个非空真子集。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：单选题

    符号“”可表示为

    A． B．
    C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    同时满足以下4个条件的集合记作：（1）所有元素都是正整数；（2）最小元素为1；（3）最大元素为2014；（4）各个元素可以从小到大排成一个公差为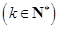的等差数列．那么中元素的个数是(  )

    A．96 B．94 C．92 D．90 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    如图是《集合》的知识结构图，如果要加入“交集”，则应该放在

    A．“集合的概念”的下位 
    B．“集合的表示”的下位 
    C．“基本关系”的下位 
    D．“基本运算”的下位 

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    下列四个集合中，表示空集的是（   ）

    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    已知集合则(    )

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知集合，
    若,则实的数取值范围是____________ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    设为两个非空集合，定义集合,若,，则中的元素个数是

    A．9 B．7 C．6 D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    关于的方程，给出下列四个命题：
    ①存在实数，使得方程恰有个不同的实根； ②存在实数，使得方程恰有个不同的实根；
    ③存在实数，使得方程恰有个不同的实根； ④存在实数，使得方程恰有个不同的实根；其中假命题的个数是（   ）

    A．个 B．个 C．个 D．个 

    查看答案和解析>>

    同步练习册答案