已知函数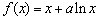
（I）当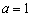
时，求曲线
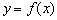在点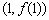
处的切线方程；
（II）求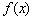
的单调区间；
（III）若函数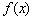没有零点，求
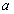的取值范围.
阅读快车系列答案科目：高中数学 来源： 题型：
某厂生产的甲、乙两种产品每件可获利润分别为30元、20元，生产甲产品每件需用A原料2 kg、B原料4 kg，生产乙产品每件需用A原料3 kg、B原料2 kg.A原料每日供应量限额为60 kg，B原料每日供应量限额为80 kg.要求每天生产的乙种产品不能比甲种产品多超过10件，则合理安排生产可使每日获得的利润最大为( )
A．500元 B．700元
C．400元 D．650元
查看答案和解析>>
科目：高中数学 来源： 题型：
已知数列{an}的前n项和Sn=2n+1-2，等差数列{bn}中，b2 = a2，面bn+3+bn-1=2bn+4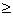, (n
2,n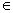
N+), 则bn=
A. 2n+2 B.2n C. n-2 D.2n-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
-
时，在
时
，所以
；
时，函数
与
在定义域上的情况如下：
∪
为椭圆
的焦点，
为椭圆上一点，
垂直于x轴，且
，则椭圆的离心率为
Ｂ．
Ｃ．
Ｄ．
存在极值，则实数
的取值范围是()
上的函数
满足：
时，
②
.
；
的零点从小到大依次记为
，则当
时，
_____________.
则z＝x＋2y的最小值为________．
＋
与N＝
的大小．