
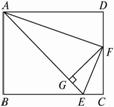
图1-10
思路分析:图中有直角三角形,充分利用直角三角形的知识,设AB=5k,BC=6k(k>0),则![]() BC =k,
BC =k, ![]() =
=![]() =3k,得DF =2k,由勾股定理可得AE2=AB2+BE2=50k2,
=3k,得DF =2k,由勾股定理可得AE2=AB2+BE2=50k2,
EF2=EC2+FC2=10k2,AF2=AD2+DF2=40k2,所以AE2=EF2+AF2.?
由勾股定理逆定理得△AFE为直角三角形,又因为FG⊥AE,具备双垂直条件,问题的解决就有了眉目.
证明:∵AB∶BC=5∶6,?
∴设AB =5k,BC =6k(k>0).?
∴在矩形ABCD中,有
CD =AB =5k,BC =AD =6k,∠B =∠C =∠D =90°.?
∵![]() ,
,
∴EC =![]() ×6k =k.?
×6k =k.?
∴BE =5k.?
∵![]() ,∴FC =
,∴FC =![]() ×5k =3k.?
×5k =3k.?
∴DF =CD -FC =2k.?
在Rt△ADF中,由勾股定理得AF2=AD2+DF2=36k2+4k2=40k2,?
同理可得AE2=50k2,EF2=10k2.?
∴AF2+EF2=40k2+10k2=50k2=AE2.?
∴△AEF是直角三角形.?
∵FG⊥AE,∴△AFE∽△FGE.?
∴EF2=GE·AE.∵![]() ,?
,?
∴![]() =
=![]() =
=![]() .?
.?
∴![]() .?
.?
∴AG =AE –GE =![]() =
=![]() .?
.?
∴AG =4GE.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
 如图所示,已知矩形ABCD中,AB=
如图所示,已知矩形ABCD中,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年吉林省高一上学期期末考试数学卷 题型:解答题
如图所示,已知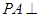 矩形ABCD所在平面,M、N分别是AB、PC的中点。
矩形ABCD所在平面,M、N分别是AB、PC的中点。
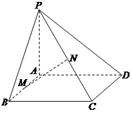
(1)求证: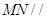 平面PAD;
平面PAD;
(2)求证: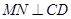
查看答案和解析>>
科目:高中数学 来源: 题型:

图1-7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com