
分析 (1)设前20天每件售价P(元)与时间x(天,x∈N+)的解析式为P=kx+b,由条件列出方程,解方程可得k,b,进而运用分段函数的解析式可得所求;
(2)运用分段函数的形式写出6月份日销售金额的解析式,再由二次函数和一次函数的性质,即可得到所求最大值.
解答 解:(1)设前20天每件售价P(元)与时间x(天,x∈N+)
的解析式为P=kx+b,
由题意可得$\left\{\begin{array}{l}{k+b=93}\\{10k+b=120}\end{array}\right.$,解得k=3.b=90,
即有该电子玩具6月份每件售价P(元)与时间x(天)的函数关系式
为P=$\left\{\begin{array}{l}{90+3x,1≤x≤20,x∈N}\\{150,21≤x≤30,x∈N}\end{array}\right.$;
(2)设6月份日销售金额为y元,即有
y=$\left\{\begin{array}{l}{(3x+90)(50-x),1≤x≤20,x∈N}\\{150(50-x),21≤x≤30,x∈N}\end{array}\right.$,
当1≤x≤20,x∈N,y=-3x2+60x+4500=-3(x-10)2+4800,
即有x=10时,取得最大值,且为4800元;
当21≤x≤30时,y=7500-150x,当x=21时,ymax=4350.
综上可得,6月份第10天的日销售金额最大,且为4800元.
点评 本题考查分段函数的应用题的解法,注意运用方程的思想和二次函数和一次函数的性质,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
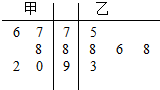 甲、乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别为x甲、x乙,则下列判断正确的是( )
甲、乙两位歌手在“中国好声音”选拔赛中,5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别为x甲、x乙,则下列判断正确的是( )| A. | x甲<x乙,甲比乙成绩稳定 | B. | x甲<x乙,乙比甲成绩稳定 | ||
| C. | x甲>x乙,甲比乙成绩稳定 | D. | x甲>x乙,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}+ln2$ | B. | $\frac{1}{2}+2ln2$ | C. | $\frac{3}{2}+2ln2$ | D. | $\frac{3}{2}+\frac{1}{2}ln2$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com