
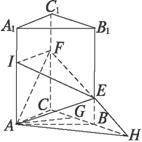
(1)求点A到侧面BB1C1C的距离;
(2)求截面AEF与底面ABC所成二面角的大小;
(3)求EF与AC所成角的余弦值.
解:(1)作AG⊥BC于G点,

∵BB1⊥平面ABC,
∴平面ABC⊥平面BB1C1C,AG⊥平面B1C1CB.
∴AG为A到侧面的距离,G在BC上.
又∵△ABC是边长为2a的正三角形,
∴G为BC的中点,AG=![]() a,即点A到侧面BB1C1C的距离为
a,即点A到侧面BB1C1C的距离为![]() a.
a.
(2)延长FE交CB的延长线于H点,连结AH,则AH=面AEF∩面ABC.
∵BE∥CF,BE=C1F=![]() CF,
CF,
∴CB=BH=AB=2a,
∠CAH=90°.
又∵CC1⊥平面ABC,
∴FA⊥AH,∠FAC为所求二面角的平面角.
在Rt△FCA中,tan∠FAC=![]() .
.
∴∠FAC=30°,即截面AEF与底面ABC成30°角.
(3)过F作FI∥AC交AA1于I点,连结IE,则∠IFE为异面直线EF与AC所成的角(或补角).
IF=2a,FE=![]() a=IE.
a=IE.
∴cos∠IFE= .
.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
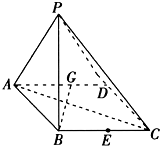 如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
如图所示,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在边长为5+
如图所示,在边长为5+| 2 |
查看答案和解析>>
科目:高中数学 来源:2013届福建省四地六校高二第一次联考理科数学 题型:解答题
(本题满分13分)
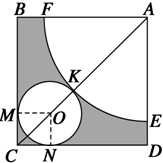
请你设计一个包装盒,如图所示,四边形ABCD是边长为60 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设 。
。
(1)某广告商要求包装盒的侧面积S 最大,试问
最大,试问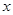 应取何值?
应取何值?
(2)某厂商要求包装盒的容积V 最大,试问
最大,试问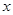 应取何值?并求出此时包装盒的高与底面边长的比值。
应取何值?并求出此时包装盒的高与底面边长的比值。


查看答案和解析>>
科目:高中数学 来源:福建省四地六校11-12学年高二下学期第一次联考试题数学理 题型:解答题
请你设计一个包装盒,如图所示,四边形ABCD是边长为60 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合与图中的点P,正好形成一个正四棱柱形状的包装盒。E,F在AB上,是被切去的一个等腰直角三角形斜边的两个端点,设 。
。
(1)某广告商要求包装盒的侧面积S 最大,试问
最大,试问 应取何值?
应取何值?
(2)某厂商要求包装盒的容积V 最大,试问
最大,试问 应取何值?并求出此时包装盒的高与底面边长的比值。
应取何值?并求出此时包装盒的高与底面边长的比值。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com