
已知函数![]() 和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(1)设![]() ,试求函数g(t)的表达式;
,试求函数g(t)的表达式;
(2)是否存在t,使得M、N与A(0,1)三点共线.若存在,求出t的值;若不存在,请说明理由.
(3)在(1)的条件下,若对任意的正整数n,在区间![]() 内总存在m+1个实数
内总存在m+1个实数![]() ,使得不等式
,使得不等式![]() 成立,求m的最大值.
成立,求m的最大值.
解:(1)设M、N两点的横坐标分别为![]() ,
,
∵![]() ,∴切线PM的方程为:
,∴切线PM的方程为:![]()
又∵切线PM过点P(1,0),∴有0-![]()
即![]() , ①
, ①
同理,由切线PN也过点P(1,0),∴![]() ②
②
由①、②,可得![]() 是方程
是方程![]() 的两根,
的两根,
∴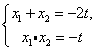 ③
③
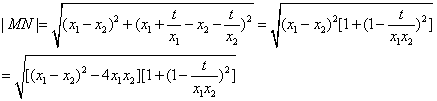 ,
,
把③式代入,得![]()
由此,函数g(t)的表达式为![]() .
.
(2)当点M、N与A共线时,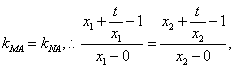
即![]() ,化简,得
,化简,得![]()
∵![]() ④
④
把③式代入④,解得t=![]() .
.
∴存在t,使得点M、N与A三点共线,且t=![]() .
.
(3)解法1:易知g(t)在区间![]() 上为增函数,
上为增函数,
∴![]()
则![]() .
.
依题意,不等式![]() 对一切的正整数n恒成立.
对一切的正整数n恒成立.
∵![]()
∴![]() .
.
由于m为正整数,∴![]()
又当![]() 时,存在
时,存在![]() ,对所有的n满足条件.
,对所有的n满足条件.
因此,m的最大值为6.
解法2:依题意,当区间![]() 的长度最小时,得到的m最大值,即是所求值.
的长度最小时,得到的m最大值,即是所求值.
∵![]() ,∴长度最小的区间为[2,16],
,∴长度最小的区间为[2,16],
当![]() 时,与解法1相同分析,得
时,与解法1相同分析,得![]()
解得![]()
后面解题步骤与解法1相同(略)


科目:高中数学 来源:2007届广东深圳市学高考数学(理科)模拟试题 题型:044
已知函数
(
Ⅰ)设|MN|=g(t),试求函数g(t)的表达式;(
Ⅱ)是否存在t,使得M、N与A(0,1)三点共线.若存在,求出t的值;若不存在,请说明理由.(
Ⅲ)在(Ⅰ)的条件下,若对任意的正整数n,在区间查看答案和解析>>
科目:高中数学 来源:浙江省杭州市2007年第二次高考科目教学质量检测数学试题卷(理科) 题型:044
已知函数![]() 和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(Ⅰ)设![]() ,试求函数g(t)的表达式;
,试求函数g(t)的表达式;
(Ⅱ)是否存在t,使得M、N与A(0,1)三点共线.若存在,求出t的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数n,在区间![]() 内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源:2008年广东地区数学科全国各地模拟试题直线与圆锥曲线大题集 题型:044
已知函数![]() 和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(Ⅰ)设|MN|=g(t),试求函数g(t)的表达式;
(Ⅱ)是否存在t,使得M、N与A(0,1)三点共线.若存在,求出t的值;若不存在,请说明理由.
(Ⅲ)在(Ⅰ)的条件下,若对任意的正整数n,在区间![]() 内总存在m+1个实数a1,a2, am,am+1,使得不等式g(a1)+g(a2)+ +g(am)<g(am+1)成立,求m的最大值.(提示::函数
内总存在m+1个实数a1,a2, am,am+1,使得不等式g(a1)+g(a2)+ +g(am)<g(am+1)成立,求m的最大值.(提示::函数![]() 的导数为
的导数为![]() )
)
查看答案和解析>>
科目:高中数学 来源:河北省衡水中学2012届高三上学期一调考试数学理科试题 题型:044
已知函数![]() 和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M(x1,y1)、N(x2,y2).
和点P(1,0),过点P作曲线y=f(x)的两条切线PM、PN,切点分别为M(x1,y1)、N(x2,y2).
(1)求证:x1,x2为关于x的方程x2+2tx-t=0的两根;
(2)设|MN|=g(t),求函数g(t)的表达式;
(3)在(2)的条件下,若在区间[2,16]内总存在m+1个实数![]() (可以相同),使得不等式
(可以相同),使得不等式![]() 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com