
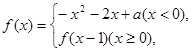
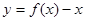 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数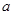 的取值范围是( )
的取值范围是( )A. | B.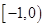 | C.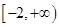 | D.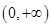 |
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
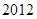 年中秋、国庆长假期间,由于国家实行
年中秋、国庆长假期间,由于国家实行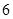 座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午
座及以下小型车辆高速公路免费政策,导致在长假期间高速公路出现拥堵现象。长假过后,据有关数据显示,某高速收费路口从上午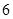 点到中午
点到中午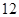 点,车辆通过该收费站的用时
点,车辆通过该收费站的用时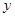 (分钟)与车辆到达该收费站的时刻
(分钟)与车辆到达该收费站的时刻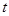 之间的函数关系式可近似地用以下函数给出:
之间的函数关系式可近似地用以下函数给出: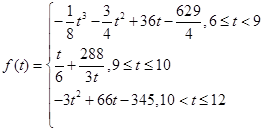
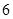 点到中午
点到中午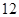 点,通过该收费站用时最多的时刻。
点,通过该收费站用时最多的时刻。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com