
 ,
,  .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
; ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 时,
时,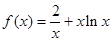 ,
, ,
,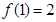 ,
,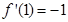 ,
, 在
在 处的切线方程为
处的切线方程为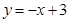 ;
;  4分
4分 ,使得
,使得 成立
成立 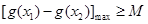 ,
, ,
,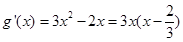 ,
,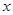 | 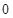 | 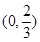 | 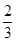 | 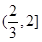 | 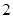 |
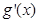 | 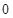 | 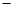 | 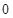 |  | |
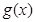 | 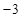 | 递减 | 极(最)小值 | 递增 | 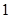 |
 ,
,
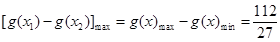 ,
,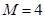 ;
; 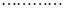 9分
9分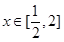 时,
时, 恒成立
恒成立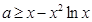 恒成立,
恒成立,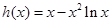 ,
, ,
, 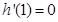 。
。 ,
,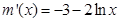 ,由于
,由于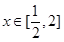 ,
,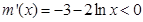 , 所以
, 所以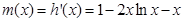 在
在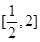 上递减,
上递减,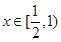 时,
时, ,
,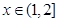 时,
时,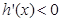 ,
,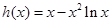 在区间
在区间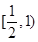 上递增,在区间
上递增,在区间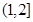 上递减,
上递减,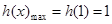 ,所以
,所以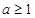 。
。 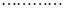 14分
14分 ,都有
,都有 成立
成立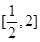 上,函数
上,函数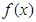 的最小值不小于
的最小值不小于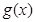 的最大值,
的最大值,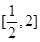 上,
上,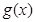 的最大值为
的最大值为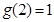 。
。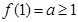 ,下证当
,下证当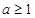 时,在区间
时,在区间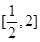 上,函数
上,函数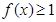 恒成立。
恒成立。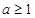 且
且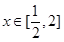 时,
时,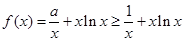 ,
,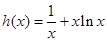 ,
,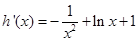 ,
, 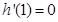
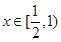 ,
,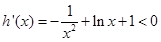 ;当
;当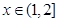 ,
,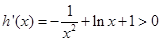 ,
,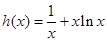 在区间
在区间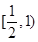 上递减,在区间
上递减,在区间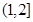 上递增,
上递增,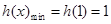 ,即
,即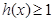 ,
, 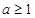 且
且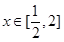 时,
时,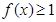 成立,
成立, ,都有
,都有 。
。  14分
14分

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:不详 题型:解答题
 (k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2011年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2011年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com