
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 (1)由q⇒p,反之不成立,可得p是q的必要不充分;
(2)p?q;
(3)对于q:方程x2-x一m=0有实根,△≥0,解得m≥-$\frac{1}{4}$,即可判断出;
(4)p:|x-1|>2?x>3或x<-1,即可判断出.
解答 解:(1)由q⇒p,反之不成立,因此p是q的必要不充分;
(2)p:xy≥0?q:|x|+|y|=|x+y|,因此p是q的充要条件;
(3)对于q:方程x2-x一m=0有实根,△=1+4m≥0,解得m≥-$\frac{1}{4}$,∴p是q的充分不必要条件;
(4)p:|x-1|>2?x>3或x<-1,p是q必要不充分条件.
其中p是q的充要条件的有1组.
故选:A.
点评 本题考查了简易逻辑的判定方法、一元二次方程有实数根与判别式的关系、不等式的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | {-2,2} | C. | {0,2} | D. | {-2,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
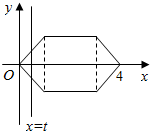 如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6
如图所示的图形由两个等腰直角三角形和一个正方形组成,且正方形的边长为2,直线x=t(0<t≤4)从左到右扫过图形的面积为S=f(t),如f(0.5)=0.25,f(4)=6查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1米 | B. | 5米 | C. | 6米 | D. | 7米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com