Question

C₁和C₂是平面上两个不重合的固定圆，C是平面上的一个动圆，C与C₁，C₂都相切，则C的圆心的轨迹是何种曲线？说明理由。

Answer 1

解：不妨设C1，C2和C的半径分别为r1，r2，r（r1>r2） （1）当C1和C2相离时，即|C1C2|>r1+r2， （i）若C与C1，C2都外切， 则|CC1|=r1+r，|CC2|=r2+r， ∴|CC1|-|CC2|=r1-r2 若C与C1，C2都内切， 则|CC1|=r-r1，|CC2|=r-r2， ∴|CC2|-|CC1|=r1-r2； ∴||CC2|-|CC1||=r1-r2<|C1C2|，由双曲线的定义，C的圆心的轨迹是以C1，C2为焦点、实轴长为r1-r2的双曲线； （ii）若C与Cl内切，C2外切， 则|CC1|=r-r1，|CC2|=r2+r， ∴|CC2|-|CC1|=r1+r2； 若C与C1外切，C2内切， 则|CC1|=r+r1，|CC2|=r-r2， ∴|CC1|-|CC2|=r1+r2 ∴||CC2|-|CC1||=r1+r2<|C1C2|，由双曲线的定义，C的圆心的轨迹是以C1，C2为焦点、实轴长为r1+r2的双曲线； （2）当C1和C2外切时，即|C1C2|=r1+r2， （i）若C与C1，C2都外切， 则|CC1|=r1+r，|CC2|=r2+r， ∴|CC1|-|CC2|=r1-r2； 若C与C1，C2都内切， 则|CC1|=r-r1，|CC2|=r-r2， ∴|CC2|-|CC1|=r1-r2； ∴||CC2|-|CC1||=r1-r2<|C1C2|，由双曲线的定义，C的圆心的轨迹是以C1，C2为焦点、实轴长为r-r2的双曲线；
（ii）若C与C1内切，C2外切， 则|CC1|=r-r1，|CC2|=r2+r（或|CC1|=r1-r，|CC2|=r2+r）（如图1，2）， ∴|CC2|-|CC1|=r1+r2（或|CC2|+|CC1|=r1+r2） 若C与C1外切，C2内切， 则|CC1|=r+r1，|CC2|=r-r2（或|CC1| =r+r1，|CC2|=r2-r）， ∴|CC1|-|CC2|=r1+r2=|C1C2|（或|CC2|+|CC1|=r1+r2= |C1C2|）， ∴C的圆心的轨迹是过C1，C2的直线（除直线与圆C1、C2的交点外）；
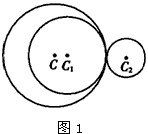（3）当C1和C2相交时， 即r1-r2<|C1C2| （i）若C与C1，C2都外切， 则|CC1|=r1+r，|CC2|=r2+r， ∴|CC1|-|CC2|=r1-r2 若C与C1，C2都内切， 则|CC1|=r-r1，|CC2|=r-r2（或|CC1| =r1-r，|CC2|=r2-r）， ∴||CC2|-|CC1|| =r1-r2 ∴||CC2|-|CC1|| =r1-r2<|C1C2|， 由双曲线的定义，C的圆心轨迹是以C1，C2为焦点、实轴长为r1-r2的双曲线（圆C1，C2的交点除外）；
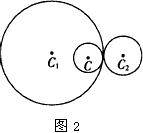
（ii）若C与C1内切，C2外切（如图3）， 则|CC1|=r1-r，|CC2|=r2+r， ∴|CC2|+|CC1|=r1+r2 若C与C1外切，C2内切， 则|CC1|=r+r1，|CC2|=r2-r， ∴|CC2|+|CC1|=r1+r2 ∴|CC2|+|CC1|=r1+r2>|C1C2|，由椭圆的定义，C的圆心的轨迹方程是以C1，C2为焦点、实轴长为r1+r2的椭圆（圆 C1、C2的交点除外）；
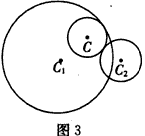（4）当C1和C2内切时， 即|C1C2| =r1-r2， （i）若C与C1，C2都外切， 则|CC1|=r1+r，|CC2|=r2+r， ∴|CC1|-|CC2|=r1-r2； 若C与C1，C2都内切， 则|CC1|=r-r1，|CC2|=r-r2（或|CC1| =r1-r，|CC2|=r-r2或|CC1|=r1-r，|CC2|=r2-r）（如图4， 5，6）， ∴|CC2|-|CC1|=r1-r2（或|CC2|+|CC1|=r1-r2或|CC2|- |CC1|=r2-r1） ∴||CC2|-|CC1||=r1-r2=|C1C2|或|CC2|+|CC1|=r1-r2， ∴C的圆心的轨迹是过C1，C2的直线（除直线与圆C1 、C2的交点外）；
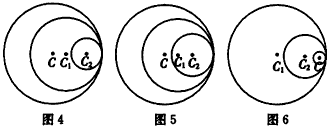（ii）若C与C1内切，C2外切， 则|CC1|=r1-r，|CC2|=r2+r， ∴|CC2|+|CC1|=r1+r2>|C1C2|， ∴C的圆心的轨迹是以C1，C2为焦点、实轴长为r1+r2的椭圆（两圆C1、C2的交点除外）；
（5）当C1和C2内含时， 即|C1C2|＜r1-r2， （i）若C与C1，C2都内切（如图7）， 则|CC1|=r1-r，|CC2|=r-r2， ∴|CC2|+|CC1|=r1-r2>|C1C2|， ∴C的圆心的轨迹是以C1，C2为焦点、实轴长为r1-r2的椭圆；
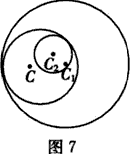（ii）若C与C1内切，C2外切， 则|CC1|=r1- r，|CC2|=r2+r， ∴|CC2|+|CC1|=r1+r2>|C1C2|， ∴C的圆心的轨迹是以C1，C2为焦点、实轴长为r1+r2的椭圆。