
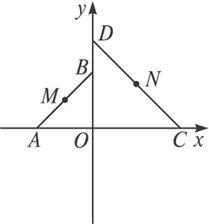
(1)若圆M与直线CD相切,求直线CD的方程.
(2)若直线AB截圆N所得弦长为4,求圆N的标准方程.
(3)是否存在这样的圆N,使得圆N上有且只有三个点到直线AB的距离为2?若存在,求此时圆N的标准方程;若不存在,请说明理由.
解:(1)圆心M(-1,1),∴圆M方程为(x+1)2+(y-1)2=2,
直线CD方程为x+y-a=0.
∵⊙M与直线CD相切,∴圆心M到直线CD的距离d=![]() =
=![]() ,
,
化简得a=±2(舍去负值).∴直线CD的方程为x+y-2=0.
(2)直线AB方程为x-y+2=0,圆心N(![]() ,
,![]() ),
),
∴圆心N到直线AB距离为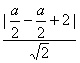 =
=![]() .
.
∵直线AB截⊙N所得弦长为4,∴22+(![]() )2=
)2=![]() .∴a=±2
.∴a=±2![]() (舍去负值).
(舍去负值).
∴⊙N的标准方程为(x-![]() )2+(y-
)2+(y-![]() )2=6.
)2=6.
(3)存在.由(2)知,圆心N到直线AB距离为![]() (定值),且AB⊥CD始终成立,
(定值),且AB⊥CD始终成立,
∴当且仅当圆N的半径![]() =2
=2![]() ,即a=4时,⊙N上有且只有三个点到直线AB的距离为2.
,即a=4时,⊙N上有且只有三个点到直线AB的距离为2.
此时⊙N标准方程为(x-2)2+(y-2)2=8.


科目:高中数学 来源: 题型:
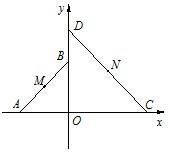 如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0),(a>0),设△AOB和△COD的
如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0),(a>0),设△AOB和△COD的查看答案和解析>>
科目:高中数学 来源: 题型:
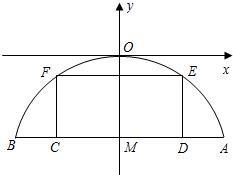 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.
(2008•江苏二模)如图,平面直角坐标系xOy中,△AOB和△COD为两等腰直角三角形,A(-2,0),C(a,0)(a>0).设△AOB和△COD的外接圆圆心分别为M,N.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中A1
(2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中A1
|
|
|
| 2 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com