
已知函数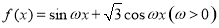 的周期为
的周期为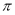 .
.

(1)若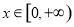 ,求它的振幅、初相;
,求它的振幅、初相;
(2)在给定的平面直角坐标系中作出该函数在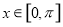 的图像;
的图像;
(3)当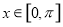 时,根据实数
时,根据实数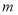 的不同取值,讨论函数
的不同取值,讨论函数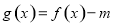 的零点个数.
的零点个数.
(1)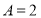 ,
,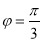 ;(2)详见解析;(3)当
;(2)详见解析;(3)当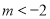 或
或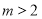 时,函数
时,函数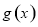 无零点;当
无零点;当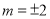 时,函数
时,函数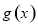 仅有一个零点;当
仅有一个零点;当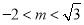 或
或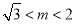 时,函数
时,函数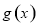 有两个零点;当
有两个零点;当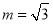 时,函数
时,函数 有三个零点.
有三个零点.
【解析】
试题分析:(1)先由辅助角公式化简,然后由周期为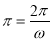 确定
确定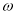 ,可确定
,可确定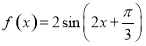 ,从而可写出振幅、初相;(2)根据正弦函数的五点作图法进行作图即可;(3)将
,从而可写出振幅、初相;(2)根据正弦函数的五点作图法进行作图即可;(3)将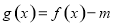 的零点问题,转化为直线
的零点问题,转化为直线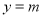 与函数
与函数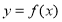 的图像交点的个数问题,结合(2)中作出的函数
的图像交点的个数问题,结合(2)中作出的函数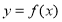 的图像,对直线的位置进行讨论,可得答案.
的图像,对直线的位置进行讨论,可得答案.
试题解析:(1)化为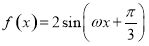 1分
1分
由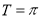 得,
得, 即
即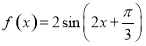 2分
2分
(1)函数的振幅是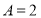 ,初相为
,初相为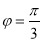 4分
4分
(2)列表
| 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2 | 0 |
| 0 |
|
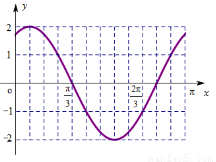 8分
8分
(3)函数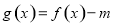 在
在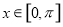 的零点个数,即函数
的零点个数,即函数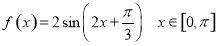 与函数
与函数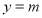 的交点个数,由(2)图像知:
的交点个数,由(2)图像知:
①当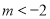 或
或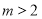 时,函数
时,函数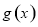 无零点;
无零点;
②当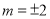 时,函数
时,函数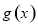 仅有一个零点;
仅有一个零点;
③当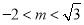 或
或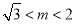 时,函数
时,函数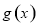 有两个零点;
有两个零点;
④当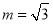 时,函数
时,函数 有三个零点 12分.
有三个零点 12分.
考点:1.辅助角公式;2.三角函数的图像与性质;3.方程的解与函数的零点.


科目:高中数学 来源:2016届福建省高一上学期期末数学试卷(解析版) 题型:选择题
设 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若 ,
, ,则
,则
②若 ,
, ,
, ,则
,则
③若 ,
, ,
, ,则
,则
④若 ,
, ,
, ,则
,则
正确命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2016届福建三明A片区高中联盟校高一上期末数学试卷(解析版) 题型:填空题
函数 有如下性质:若常数
有如下性质:若常数 ,则函数在
,则函数在 上是减函数,在
上是减函数,在 上是增函数。已知函数
上是增函数。已知函数 (
( 为常数),当
为常数),当 时,若对任意
时,若对任意 ,都有
,都有 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2016届湖南省高一上学期期末考试数学试卷(解析版) 题型:填空题
如图,二面角 的大小是60°,线段
的大小是60°,线段 在平面EFGH上,
在平面EFGH上, 在EF上,
在EF上, 与EF所成的角为30°,则
与EF所成的角为30°,则 与平面
与平面 所成的角的正弦值是__________.
所成的角的正弦值是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com