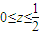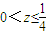已知实数x,y,z满足xyz=32,x+y+z=4,则|x|+|y|+|z|的最小值为________.
12
分析:为了去掉绝对值,先讨论三个实数的符号一定为一正二负,从而将|x|+|y|+|z|转化为关于x的函数,再利用判别式法求x的范围,即可得所求
解答:不妨设x≥y≥z由于xyz=32>0所以x,y,z要么满足全为正,要么一正二负
若是全为正数,由均值不等式得:4=x+y+z≥3
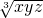
,所以xyz≤

<32,矛盾.
所以必须一正二负.即x>0>y≥z
从而|x|+|y|+|z|=x-y-z=2x-(x+y+z)=2x-4,所以只要x最小
将z=4-x-y代入xyz=32得:xy
2+(x
2-4x)y-32=0
由△≥0,得:(x
2-4x)
2≥128x
即x(x-8)(x
2+16)≥0因为x>0,x
2+16>0,所以一定有x-8≥0,x≥8
所以|x|+|y|+|z|的最小值为2×8-4=12
故答案为12
点评:本题考查了推理论证能力,均值定理的运用,含绝对值函数问题的解决方法,判别式法求变量的取值范围

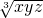 ,所以xyz≤
,所以xyz≤ <32,矛盾.
<32,矛盾.

 ,则z的取值范围是( )
,则z的取值范围是( )