
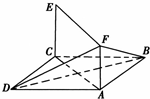
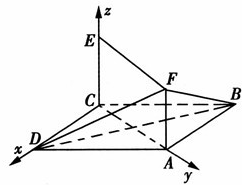
 如图所示,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,ADC=60°,AF=
如图所示,已知平行四边形ABCD和平行四边形ACEF所在的平面相交于直线AC,EC⊥平面ABCD,AB=1,AD=2,ADC=60°,AF=| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| n |
| m |
| DF |
| 3 |
| 3 |
| DB |
| 3 |
|
|
| m |
| 3 |
| m |
| n |
| ||||
|
|
| ||
| 4 |
| ||
| 4 |


科目:高中数学 来源: 题型:
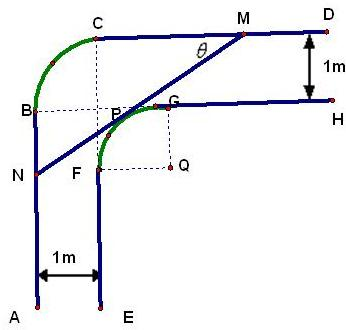 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分16分)
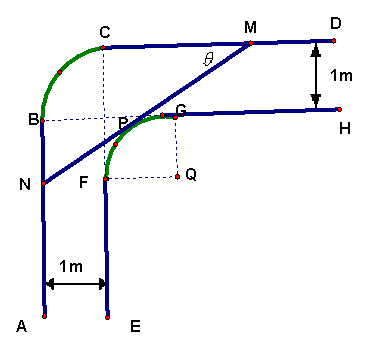
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
若水平放置的木棒MN的两个端点M、N分别在外壁CD和AB上,且木棒与内壁圆弧相切于点P。设![]() ,试用
,试用![]() 表示木棒MN和长度
表示木棒MN和长度![]() 。
。
若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值。
查看答案和解析>>
科目:高中数学 来源:2010年江苏省苏北四市高考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年江苏省徐州市高考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com