
已知动点P(x,y)满足约束条件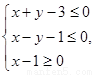 ,O为坐标原点,定点A(6,8),则
,O为坐标原点,定点A(6,8),则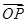 在
在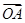 上的投影的范围
上的投影的范围
A.[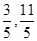 ] B.[
] B.[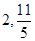 ] C.
] C. D.[
D.[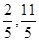 ]
]
A
【解析】解:在平面直角坐标系中画出不等式组所表示的可行域(如图),
由于| OP |•cos∠AOP=[| OP |•| OA |cos∠AOP] ]/ OA |= OP • OA /| OA | ,而 OA =(6,8), OP =(x,y),OA的长度为10
所以| OP |•cos∠AOP=6x+8y /10 ,
令z=6x+8y,即z表示直线y=-6/ 8 x+1/ 4 z在y轴上的截距,
由图形可知,当直线经过可行域中的点B时,z取到最小值,
由B(1,0),这时z=3,
所以| OP |•cos∠AOP=3 /5 ,
故| OP |•cos∠AOP的最小值等于 3/ 5 .
由图形可知,当直线经过可行域中的点C时,z取到最大值,
由C(2,1),这时z=10,
所以| OP |•cos∠AOP=2,
故| OP |•cos∠AOP的最大值等于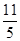 .
.
故答案为A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 16 |
| MF |
| MP |
| MF |
| PM |
A、
| ||
| B、3 | ||
C、
| ||
| D、1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com