
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |

 的概率;
的概率; 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。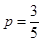 ;(3)
;(3)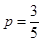
 的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在 的频率
的频率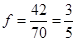
 -----------------------------------------6分
-----------------------------------------6分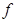 估计该校学生身高在
估计该校学生身高在 的概率
的概率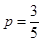 .--------------------8分
.--------------------8分 185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185
185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185 190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为: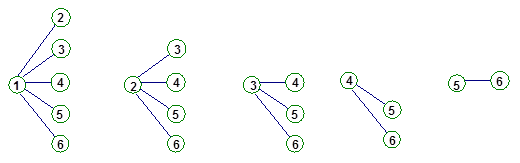 10分
10分 190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185
190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185 190cm之间的可能结果数为9,因此,所求概率
190cm之间的可能结果数为9,因此,所求概率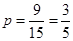 .---------------12分
.---------------12分

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源:不详 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
; )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是( )
,据此可以预测这个孩子10岁时的身高,则正确的叙述是( ) | A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 转速χ(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入(单位百元) | [15,25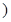 | [25,35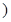 | [35,45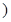 | [45,55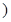 | [55,65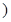 | [65,75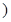 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 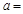 3 3 | 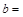 | |
| 不赞成 | 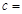 | 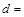 11 11 | |
| 合计 | | | 50 |
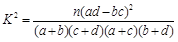 ,其中
,其中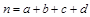 .)
.)P(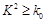 ) ) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
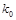 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
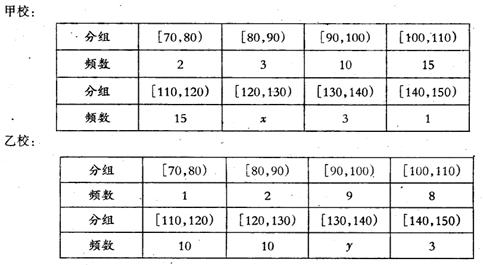
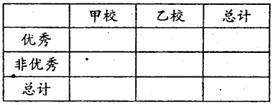
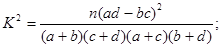
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
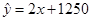 ,则当用水量为50kg时,预计的某种产品的产量是( )
,则当用水量为50kg时,预计的某种产品的产量是( ) | A.大于1350kg | B.小于 1350kg | C.1350kg | D.以上都不对 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
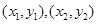 ,…,
,…,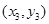 是变量
是变量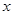 和
和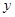 的
的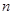 个样本点,直线
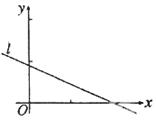
个样本点,直线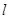 是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是 ( )
是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是 ( )A.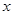 和 和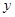 的相关系数为直线 的相关系数为直线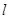 的斜率 的斜率 |
B.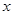 和 和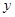 的相关系数在0到1之间 的相关系数在0到1之间 |
C.当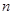 为偶数时,分布在 为偶数时,分布在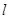 两侧的样本点的个数一定相同 两侧的样本点的个数一定相同 |
D.直线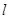 过点 过点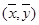 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题

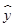 =bx+a必过的点是
=bx+a必过的点是| A.(2,2) | B.(1,2) | C.(3,4) | D.(4,5) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com