D
分析:对于二项展开式两边同时取导数,令x=1 可得 a
1+2a
2+3a
3+4a
4+…+9a
9=3
10.令x=-1可得a
1-2a
2+3a
3-4a
4+…+9a
9=9,再由所求的式子等于(a
1-2a
2+3a
3-4a
4+…+9a
9 )(a
1+2a
2+3a
3+4a
4+…+9a
9),运算求得结果.
解答:∵已知
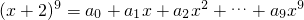
,
两边同时取导数可得9(x+2)
8=a
1+2a
2•x+3a
3•x
2+4a
4•x
3+…+9a
9x
8.
令x=1 可得 a
1+2a
2+3a
3+4a
4+…+9a
9=3
10.
在 9(x+2)
8=a
1+2a
2•x+3a
3•x
2+4a
4•x
3+…+9a
9x
8 中,令x=-1可得
得 a
1-2a
2+3a
3-4a
4+…+9a
9=9.
故所求的式子等于 (a
1-2a
2+3a
3-4a
4+…+9a
9 )(a
1+2a
2+3a
3+4a
4+…+9a
9)
=9×3
10=3
12,
故选D.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,可以简便的求出答案,属于中档题.

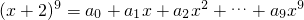 ,则
,则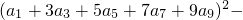 (2a2+
(2a2+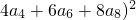 的值为
的值为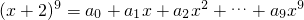 ,
,

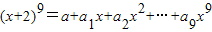 ,则
,则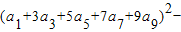 (2a2+
(2a2+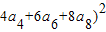 的值为( )
的值为( )