考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:(1))由∠C=2∠A,得到∠B=π-3∠A,再由诱导公式和二倍角公式及两角和的余弦公式,即可得到cos∠B的值;
(2)由cos∠A=
,得到sin∠A,再求得sinC,由正弦定理求出
,再由平面向量的数量积的定义,可得ac的值,解出a,c,再由余弦定理,即可得到b.
解答:
解:(1)∵∠C=2∠A,
∴∠B=π-∠A-∠C=π-3∠A,
∴cos∠B=-cos3∠A=-cos(2∠A+∠A)
=-(cos2∠Acos∠A-sin2∠Asin∠A)
=-(2cos
3∠A-cos∠A-2sin
2∠Acos∠A)
=3cos∠A-4cos
3∠A
=3×
-4×(
)
3=
;
(2)由cos∠A=
,则sin∠A=
=
,
sinC=sin2∠A=2sin∠Acos∠A=2×
×=
,
由正弦定理可得,
=
=
,
由
•
=
,得cacos∠B=
,
则ac=
×=24,
即有a=4,c=6,
则由余弦定理得,b
2=a
2+c
2-2accos∠B=16+36-2×4×6×
=25,
则b=5.
故边AC的长为5.
点评:本题考查三角函数的化简和求值,考查余弦定理和正弦定理及运用,平面向量的数量积的运用,考查三角函数的恒等变换的运算能力,属于中档题.



 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案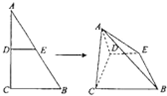 直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.
直角三角形ABC中,∠ACB=90°,AB=2BC=2,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使△ADE沿DE折起,使△ADC为等边三角形,如图所示.