
A.①和② B.③和④ C.①和④ D.②和③
解析:(1)当k=2n时,sin(kπ+![]() )=sin(2nπ+
)=sin(2nπ+![]() )=sin
)=sin![]() .
.
当k=2n+1时,sin(kπ+![]() )=sin[(2n+1)π+
)=sin[(2n+1)π+![]() ]=sin(2nπ+π+
]=sin(2nπ+π+![]() )=sin(π+
)=sin(π+![]() )=-sin
)=-sin![]() .
.
(2)sin(2kπ±![]() )=sin(±
)=sin(±![]() )=±sin
)=±sin![]() .
.
(3)当k=2n时,sin[kπ+(-1)k·![]() ]=sin[2nπ+(-1)2n·
]=sin[2nπ+(-1)2n·![]() ]=sin
]=sin![]() .
.
当k=2n+1时,sin[kπ+(-1)k·![]() ]=sin[2nπ+π-
]=sin[2nπ+π-![]() ]=sin
]=sin![]() .
.
(4)cos[2kπ+(-1)k·![]() ]=cos[(-1)k·
]=cos[(-1)k·![]() ].
].
当k=2n时,原式=cos![]() =sin
=sin![]() .
.
当k=2n+1时,原式=cos[(-1)2n+1·![]() ]=cos
]=cos![]() =sin
=sin![]() .故选B.
.故选B.
答案:B


科目:高中数学 来源: 题型:
 如图,已知双曲线C1:
如图,已知双曲线C1:| y2 |
| m |
| x2 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求双曲线S的方程;
(2)当k=1时,在双曲线S的上支上求点B,使其与直线l的距离为![]() ;
;
(3)当0≤k<1时,若双曲线S的上支上有且只有一个点B到直线l的距离为![]() ,求斜率k的值及相应的点B的坐标.
,求斜率k的值及相应的点B的坐标.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高一上学期期末模拟数学试卷(解析版) 题型:填空题
对于函数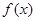 =
= ,给出下列四个命题:
,给出下列四个命题:
①该函数是以 为最小正周期的周期函数;
为最小正周期的周期函数;
②当且仅当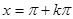 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1;
③该函数的图象关于 (k∈Z)对称;
(k∈Z)对称;
④当且仅当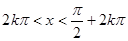 (k∈Z)时,0<
(k∈Z)时,0<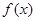 ≤
≤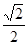 .
.
其中正确命题的序号是________ (请将所有正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com